Successió de Farey

En matemàtiques, la seqüència de Farey o successió de Farey d'ordre n és la seqüència de les fraccions irreductibles entre 0 i 1, o sense aquesta restricció,^{[Nota 1]} en la qual el denominador és inferior o igual a n i en ordre creixent.

• 
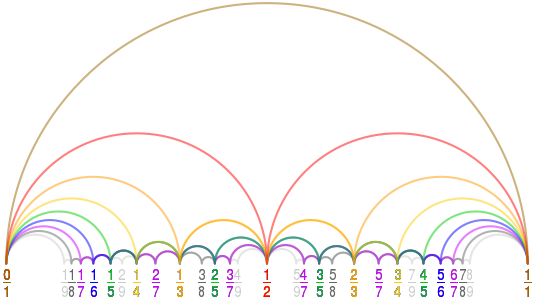  Diagrama de Farey a F₉ representat amb arcs circulars. A la imatge SVG, passeu el cursor per sobre d'una corba per ressaltar-la i els seus termes.
• 
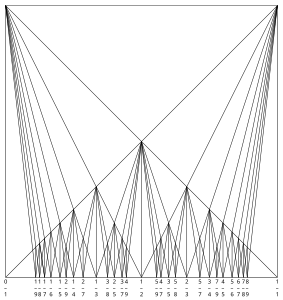  Diagrama de Farey a F₉

Qualsevol successió comença amb el valor 0, representat per la fracció ⁰⁄₁, i finalitza amb el valor 1, representat per la fracció ¹⁄₁ (tot i que certs autors ometen aquest terme).

• 
  Patró simètric fet pels denominadors de la seqüència de Farey, F₉

De vegades aquesta successió rep el nom de sèrie de Farey, però això no és estrictament correcte atès que els termes no se sumen.

• 
  Patró simètric fet pels denominadors de la seqüència de Farey, F₂₅

Porta el nom del seu inventor, el geòleg anglès John Farey (1766-1826). El 1924, el matemàtic suís Jérôme Franel, va trobar una subtil relació entre la sèrie de Farey i la Hipòtesi de Riemann, cosa que va fer que Edmund Landau investigués aquesta relació, publicant un parell d'articles sobre el tema.^[1][2]

Exemples

Les seqüències de Farey d'ordres de l'1 al 8 són:

F₁ = { 0/1_, 1/1 }

F₂ = { 0/1_, 1/2_, 1/1 }

F₃ = { 0/1_, 1/3_, 1/2_, 2/3_, 1/1 }

F₄ = { 0/1_, 1/4_, 1/3_, 1/2_, 2/3_, 3/4_, 1/1 }

F₅ = { 0/1_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 1/1 }

F₆ = { 0/1_, 1/6_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 5/6_, 1/1 }

F₇ = { 0/1_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 1/1 }

F₈ = { 0/1_, 1/8_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 3/8_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 5/8_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 7/8_, 1/1 }

 F1 = {0/1,                                                                                                          1/1}
 F2 = {0/1,                                                   1/2,                                                   1/1}
 F3 = {0/1,                               1/3,                1/2,                2/3,                               1/1}
 F4 = {0/1,                     1/4,      1/3,                1/2,                2/3,      3/4,                     1/1}
 F5 = {0/1,                1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5,                1/1}
 F6 = {0/1,           1/6, 1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5, 5/6,           1/1}
 F7 = {0/1,      1/7, 1/6, 1/5, 1/4, 2/7, 1/3,      2/5, 3/7, 1/2, 4/7, 3/5,      2/3, 5/7, 3/4, 4/5, 5/6, 6/7,      1/1}
 F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

Gràfica «esclat solar» de Farey

Traçant els numeradors en funció dels denominadors d'una seqüència de Farey s'obté una forma com els gràfics inferiors.

• 
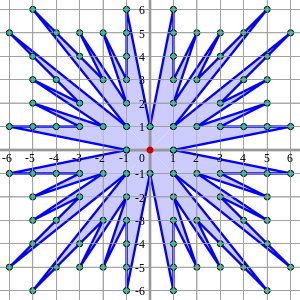  Gràfica «esclat solar» de Farey d'ordre 6, amb 1 interior (vermell) i 96 punts de límit (verd) donant una àrea d'1 + 96/2 − 1 = 48, segons el teorema de Pick
• 
  Iteracions 1-10

En reflectir aquesta forma al voltant dels eixos diagonal i principal es genera la gràfica «esclat solar» de Farey. L'esclat solar Farey d'ordre n connecta els punts de la quadrícula d'enters visibles des de l'origen al quadrat del costat 2n, centrats a l'origen. Utilitzant el teorema de Pick, l'àrea de l'esclat solar és 4(|F_n|−1), on |F_n| és el nombre de fraccions en F_n.

Història

Les seqüències de Farey reben el nom del geòleg britànic John Farey, Sr., la carta del qual sobre aquestes seqüències es va publicar a la revista Philosophical Magazine el 1816.^[3] Farey va conjecturar, sense oferir proves, que cada nou terme en una expansió de la seqüència de Farey és el mediant dels seus veïns. Cauchy va llegir la carta de Farey, que va aportar una prova en els seus Exercices de mathématique, i va atribuir aquest resultat a Farey.

De fet, un altre matemàtic, Charles Haros, havia publicat resultats similars el 1802 que no eren coneguts ni per Farey ni per Cauchy.^[4] Així, va ser un accident històric el que va vincular el nom de Farey amb aquestes seqüències. Aquest és un exemple de la Llei de Stigler.

Propietats

• 
  Diagrama de Farey amb cercles, ordre F₄
• 
  Diagrama de Farey amb cercles, ordre F₆

Longitud de la seqüència i índex d'una fracció

La seqüència de Farey d'ordre n conté tots els membres de les seqüències de Farey d'ordre inferior. En particular F_n conté tots els membres de F_n−1 i també conté una fracció addicional per a cada nombre que sigui menor que n i coprimer a n. Així F₆ està format per F₅ juntament amb les fraccions 1/6 i 5/6.

El terme mig d'una seqüència de Farey F_n és sempre 1/2, per a n > 1. A partir d'això, podem relacionar les longituds de F_n i F_n−1 utilitzant la funció φ d'Euler ${\displaystyle \varphi (n)}$:

${\displaystyle |F_{n}|=|F_{n-1}|+\varphi (n).}$

Utilitzant el fet que |F₁| = 2, podem derivar una expressió per a la longitud de F_n:^[5]

${\displaystyle |F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\Phi (n),}$

on ${\displaystyle \Phi (n)}$ és la suma indicatriu.

També tenim:

${\displaystyle |F_{n}|={\frac {1}{2}}\left(3+\sum _{d=1}^{n}\mu (d)\left\lfloor {\tfrac {n}{d}}\right\rfloor ^{2}\right),}$

i mitjançant una fórmula d'inversió de Möbius:

${\displaystyle |F_{n}|={\frac {1}{2}}(n+3)n-\sum _{d=2}^{n}|F_{\lfloor n/d\rfloor }|,}$

on µ(d) és el nombre teòric de la funció de Möbius, i ${\displaystyle \lfloor {\tfrac {n}{d}}\rfloor }$ és la funció de part entera.

El comportament asimptòtic de |F_n| és:

${\displaystyle |F_{n}|\sim {\frac {3n^{2}}{\pi ^{2}}}.}$

L'índex ${\displaystyle I_{n}(a_{k,n})=k}$ d'una fracció ${\displaystyle a_{k,n}}$ en la seqüència de Farey ${\displaystyle F_{n}=\{a_{k,n}:k=0,1,\ldots ,m_{n}\}}$ és simplement la posició que ${\displaystyle a_{k,n}}$ ocupa en la seqüència. Això és d'especial rellevància, ja que s'utilitza en una formulació alternativa de la hipòtesi de Riemann (vegeu més avall). A continuació es mostren diverses propietats útils:

${\displaystyle I_{n}(0/1)=0,}$

${\displaystyle I_{n}(1/n)=1,}$

${\displaystyle I_{n}(1/2)=(|F_{n}|-1)/2,}$

${\displaystyle I_{n}(1/1)=|F_{n}|-1,}$

${\displaystyle I_{n}(h/k)=|F_{n}|-1-I_{n}((k-h)/k).}$

L'índex d' ${\displaystyle 1/k}$ on ${\displaystyle n/(i+1)<k\leq n/i}$ i ${\displaystyle n}$ és el mínim comú múltiple del primer ${\displaystyle i}$ nombre, ${\displaystyle n={\rm {mcm}}([2,i])}$, ve donat per:^[6]

${\displaystyle I_{n}(1/k)=1+n\sum _{j=1}^{i}{\frac {\varphi (j)}{j}}-k\Phi (i).}$

Termes veïns de Farey

Les fraccions que són termes veïns en qualsevol seqüència de Farey es coneixen com a parell de Farey i tenen les propietats següents:

Si a/b i c/d són veïns en una seqüència de Farey, amb a/b < c/d, llavors la seva diferència c/d − a/b és igual a 1/bd. Això es deu al fet que cada parell consecutiu de racionals de Farey té una àrea equivalent a 1.^[7]

Si r₁=p/q i r₂=p'/q' s'interpreten com a vectors (p,q) en el pla x,y, l'àrea de A(p/q,p'/q') està donat per qp' - q'p. Com que qualsevol fracció afegida entre dues fraccions de seqüències de Farey consecutives anteriors es calcula com a mediant (⊕)

A(r₁,r₁⊕r₂) = A(r₁,r₁) + A(r₁,r₂) = A(r₁,r₂) = 1 (a partir de r₁=1/0 i r₂=0/1 la seva àrea ha de ser 1).

Des de:${\displaystyle {\frac {c}{d}}-{\frac {a}{b}}={\frac {bc-ad}{bd}},}$

això equival a dir això

${\displaystyle bc-ad=1}$.

Així 1/3 i 2/5 són veïns F₅, i la seva diferència és 1/15.

El contrari també és cert. Si

${\displaystyle bc-ad=1}$

per a nombres enters positius a,b,c i d amb a < b i c < d llavors a/b i c/d seran els veïns de la seqüència d'ordre Farey max(b,d).

Si p/q és veí de a/b i c/d en alguna seqüència de Farey, amb

${\displaystyle {\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}}$

llavors p/q és la fracció mediant de a/b i c/d ; en altres paraules,

${\displaystyle {\frac {p}{q}}={\frac {a+c}{b+d}}.}$

Això es desprèn fàcilment de la propietat anterior, ja que si bp – aq = qc – pd = 1, llavors bp + pd = qc + aq, p(b + d) = q(a + c), p/q = a + c/b + d.

Es dedueix que si a/b i c/d són veïns d'una seqüència de Farey, llavors el primer terme que apareix entre ells a mesura que s'incrementa l'ordre de la seqüència de Farey és

${\displaystyle {\frac {a+c}{b+d}},}$

que apareix per primera vegada a la seqüència de Farey d'ordre b + d.

Així el primer terme que apareix entre 1/3 i 2/5 és 3/8, que apareix a F₈.

El nombre total de parelles de veïns de Farey F_n és 2|F_n|-3.

L'arbre Stern-Brocot és una estructura de dades que mostra com es construeix la seqüència 0 (= 0/1) i 1 (= 1/1), prenent mediants successius.

Veïns de Farey i fraccions contínues

Les fraccions que apareixen com a veïnes en una seqüència de Farey tenen expansions de fraccions contínues estretament relacionades. Cada fracció té dues expansions de fraccions contínues: en una, el terme final és 1; en l'altre el termini final és superior a 1. Si p/q, que apareix per primera vegada a la seqüència de Farey F_q, té expansions de fraccions contínues

[0; a₁, a₂, ..., a_{n − 1}, a_n, 1]

[0; a₁, a₂, ..., a_{n − 1}, a_n + 1]

llavors el veí més proper de p/q en F_q (que serà el seu veí amb el denominador més gran) té una expansió de fracció contínua

[0; a₁, a₂, ..., a_n]

i el seu altre veí té una expansió continuada de fraccions

[0; a₁, a₂, ..., a_{n − 1}]

Per exemple, 3/8 té les dues expansions de fraccions contínues [0; 2, 1, 1, 1] i [0; 2, 1, 2], i els seus veí en F₈ és 2/5, que es pot ampliar com [0; 2, 1, 1]; i 1/3, que es pot ampliar com [0; 2, 1].

Fraccions de Farey i el mínim comú múltiple

El mcm es pot expressar com els productes de les fraccions de Farey com

${\displaystyle {\text{mcm}}[1,2,...,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2}}$

on ${\displaystyle \psi (N)}$ és la segona funció de Chebyshev.^[8][9]

Fraccions de Farey i màxim comú divisor

Com que la funció φ d'Euler està directament connectada amb el mcd, també ho és el nombre d'elements a F_n.

${\displaystyle |F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\sum \limits _{m=1}^{n}\sum \limits _{k=1}^{m}{\text{mcd}}(k,m)\cos {2\pi {\frac {k}{m}}}.}$

Per a tres fraccions de Farey qualsevol a/b, c/d i e/f la següent identitat entre els mcd dels determinants de la matriu 2x2 en valor absolut es compleix:^[10]

${\displaystyle {\text{mcd}}\left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}a&e\\b&f\end{Vmatrix}}\right)={\text{mcd}}\left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)={\text{mcd}}\left({\begin{Vmatrix}a&e\\b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)}$^[6]

Aplicacions

Les seqüències de Farey són molt útils per trobar aproximacions racionals de nombres irracionals.^[11] Per exemple, la construcció per Eliahou^[12] d'un límit inferior de la durada dels cicles no trivials en el procés 3x+1 utilitza seqüències de Farey per calcular una expansió de fracció contínua del nombre log₂(3).

En sistemes físics amb fenòmens de ressonància, les seqüències de Farey proporcionen un mètode molt elegant i eficient per calcular ubicacions de ressonància en 1D^[13] i 2D.^[14]

Les seqüències de Farey són destacades en els estudis de planificació de camins de qualsevol angle en quadrícules de cel·les quadrades, per exemple en caracteritzar la seva complexitat computacional^[15] o optimitat.^[16] La connexió es pot considerar en termes de camins r-restringits, és a dir, camins formats per segments de línia que travessen cadascun com a màxim ${\displaystyle r}$ files i com a màxim ${\displaystyle r}$ columnes de cel·les. Sigui ${\displaystyle Q}$ el conjunt de vectors ${\displaystyle (q,p)}$ tal que ${\displaystyle 1\leq q\leq r}$, ${\displaystyle 0\leq p\leq q}$, i ${\displaystyle p}$, ${\displaystyle q}$ són coprimers. Sigui ${\displaystyle Q*}$ el resultat del reflex ${\displaystyle Q}$ en la línea ${\displaystyle y=x}$. Sigui ${\displaystyle S=\{(\pm x,\pm y):(x,y)\in Q\cup Q*\}}$. Aleshores, qualsevol camí r-restringit per r es pot descriure com una seqüència de vectors a partir de ${\displaystyle S}$. Hi ha una bijecció entre ${\displaystyle Q}$ i la seqüència de Farey d'ordre ${\displaystyle r}$ donat per ${\displaystyle (q,p)}$ mapejat a ${\displaystyle {\tfrac {p}{q}}}$.

Per a cercles de Ford

Hi ha una connexió entre la seqüència de Farey i els cercles de Ford.

Per cada fracció p/q (en els seus termes més baixos) hi ha un cercle de Ford C[p/q], que és el cercle amb radi 1/(2q²) i el centre a (p/q, 1/ 2q² ). Dos cercles de Ford per a diferents fraccions són disjunts o tangents entre si; dos cercles de Ford mai es tallen. Si 0 < p/q < 1 llavors els cercles de Ford que són tangents a C[p/q] són precisament els cercles de Ford per a les fraccions que són veïnes de p/q en alguna seqüència de Farey.

• 
  Comparació de cercles de Ford i un diagrama de Farey amb arcs circulars per a n d'1 a 9. Cada arc talla els seus cercles corresponents en angle recte. A la imatge SVG, passeu el cursor per sobre d'un cercle o una corba per ressaltar-lo i els seus termes
• 
  Tamís d'Apol·loni (0,0,1,1) i el diagrama de ressonància de Farey

Així C[2/5] és tangent a C[1/2], C[1/3], C[3/7], C[3/8] etc.

Els cercles de Ford també apareixen al tamís d'Apol·loni (0,0,1,1). La imatge superior ho il·lustra juntament amb les línies de ressonància de Farey.^[10]

Hipòtesi de Riemann

Les seqüències de Farey s'utilitzen en dues formulacions equivalents de la hipòtesi de Riemann. Suposem els termes de ${\displaystyle F_{n}}$ són ${\displaystyle \{a_{k,n}:k=0,1,\ldots ,m_{n}\}}$. Definim ${\displaystyle d_{k,n}=a_{k,n}-k/m_{n}}$, el altres paraules ${\displaystyle d_{k,n}}$ és la diferència entre el terme k-èssim de l'enèsima seqüència de Farey i el k-è membre d'un conjunt del mateix nombre de punts, distribuïts uniformement en l'interval unitari. El 1924 Jérôme Franel va demostrar que la declaració.^[17]

${\displaystyle \sum _{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r})\quad \forall r>-1}$

és equivalent a la hipòtesi de Riemann, i llavors Edmund Landau va remarcar (just després de l'article de Franel) que l'afirmació^[18]

${\displaystyle \sum _{k=1}^{m_{n}}|d_{k,n}|=O(n^{r})\quad \forall r>1/2}$

també és equivalent a la hipòtesi de Riemann.

Altres sumes que impliquen fraccions de Farey

La suma de totes les fraccions de Farey d'ordre n és la meitat del nombre d'elements:

${\displaystyle \sum _{r\in F_{n}}r={\frac {1}{2}}|F_{n}|.}$

La suma dels denominadors de la seqüència de Farey és el doble de la suma dels numeradors i es relaciona amb la funció φ d'Euler:

${\displaystyle \sum _{a/b\in F_{n}}b=2\sum _{a/b\in F_{n}}a=1+\sum _{i=1}^{n}i\varphi (i),}$

que va ser conjecturada per Harold L. Aaron el 1962 i demostrada per Jean A. Blake el 1966. Una prova d'una línia de la conjectura de Harold L. Aaron és la següent.

La suma dels numeradors és ${\displaystyle {\displaystyle 1+\sum _{2\leq b\leq n}\sum _{(a,b)=1}a=1+\sum _{2\leq b\leq n}b{\frac {\varphi (b)}{2}}}}$. La suma dels denominadors és ${\displaystyle {\displaystyle 2+\sum _{2\leq b\leq n}\sum _{(a,b)=1}b=2+\sum _{2\leq b\leq n}b\varphi (b)}}$. El quocient de la primera suma per la segona suma és ${\displaystyle {\frac {1}{2}}}$.

Siguin b_j els denominadors ordenats de F_n, llavors:^[19]

${\displaystyle \sum _{j=0}^{|F_{n}|-1}{\frac {b_{j}}{b_{j+1}}}={\frac {3|F_{n}|-4}{2}}}$

i

${\displaystyle \sum _{j=0}^{|F_{n}|-1}{\frac {1}{b_{j+1}b_{j}}}=1.}$

Siguin a_j/b_j la j-ena fraccion de Farey en F_n, llavors

${\displaystyle \sum _{j=1}^{|F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\sum _{j=1}^{|F_{n}|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1}\end{Vmatrix}}=3(|F_{n}|-1)-2n-1,}$

que es demostra a [Hall, Shiu 2003, p. 2009-223].^[20] També segons aquesta referència el terme dins de la suma es pot expressar de moltes maneres diferents:

${\displaystyle a_{j-1}b_{j+1}-a_{j+1}b_{j-1}={\frac {b_{j-1}+b_{j+1}}{b_{j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j-1}}{b_{j}}}\right\rfloor ,}$

obtenint així moltes sumes diferents sobre els elements de Farey amb el mateix resultat. Utilitzant la simetria al voltant de 1/2, la suma anterior es pot limitar a la meitat de la seqüència com

${\displaystyle \sum _{j=1}^{\lfloor |F_{n}|/2\rfloor }(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=3(|F_{n}|-1)/2-n-\lceil n/2\rceil ,}$

La funció de Mertens es pot expressar com una suma sobre fraccions de Farey com

${\displaystyle M(n)=-1+\sum _{a\in {\mathcal {F}}_{n}}e^{2\pi ia}}$ on ${\displaystyle {\mathcal {F}}_{n}}$ és la seqüència de Farey d'ordre n.

Aquesta fórmula s'utilitza en la demostració del teorema de Franel-Landau.^[21]

El terme següent

Existeix un algorisme sorprenentment senzill per generar els termes de F_n en ordre tradicional (creixent) o en ordre no tradicional (descendent). L'algorisme calcula cada entrada successiva en termes de les dues entrades anteriors utilitzant la propietat mediant donada anteriorment. Si a/b i c/d  són les dues entrades donades, i p/q és la següent entrada desconeguda, llavors c/d = a + p/b + q. A partir de c/d  és en termes més baixos, ha d'haver un nombre enter k tal que kc = a + p i kd = b + q, donant p = kc − a i q = kd − b. Si considerem que p i q són funcions de k, aleshores

${\displaystyle {\frac {p(k)}{q(k)}}-{\frac {c}{d}}={\frac {cb-da}{d(kd-b)}}}$

per tant, com més gran és k, més a prop p/q arriba a c/d.

Per donar el següent terme de la seqüència, k ha de ser el més gran possible, subjecte a kd − b ≤ n (ja que només estem considerant nombres amb denominadors no superiors a n), de manera que k és el nombre enter més gran ≤n + b/d. Si tornem a posar aquest valor de k a les equacions de p i q, s'obté

${\displaystyle p=\left\lfloor {\frac {n+b}{d}}\right\rfloor c-a}$

${\displaystyle q=\left\lfloor {\frac {n+b}{d}}\right\rfloor d-b}$

Això s'implementa a Python de la següent manera:

def farey_sequence(n: int, descending: bool = False) -> None:
    """Imprimeix la seqüència enèima de Farey. Permet pujar o baixar."""
    (a, b, c, d) = (0, 1, 1, n)
    if descending:
        (a, c) = (1, n - 1)
    print("{0}/{1}".format(a, b))
    while (c <= n and not descending) or (a > 0 and descending):
        k = (n + b) // d
        (a, b, c, d) = (c, d, k * c - a, k * d - b)
        print("{0}/{1}".format(a, b))

Les cerques de força bruta per a solucions d'equacions diofàntiques en racionals sovint poden aprofitar la sèrie de Farey (per cercar només formes reduïdes). Les línies marcades amb (*) també es poden modificar per incloure dos termes adjacents qualsevol per generar termes només més grans (o més petits) que un terme determinat.^[22]

Notes

Referències

Bibliografia

Vegeu també

• Arbre de Stern-Brocot
• Funció φ d'Euler
• Funció signe d'interrogació

Enllaços externs

• «Farey series» (en anglès). EMS Press, 2001 [1994].
• OEIS successió A005728 (nombre de fraccions de la sèrie de Farey d'ordre n)
• Vepstas, Linas. «The Minkowski Question Mark, GL(2,Z), and the Modular Group» (PDF) (en anglès). Revisa els isomorfismes de l'arbre de Stern-Brocot.