Normalkraft
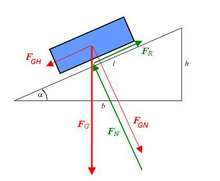
Als Normalkraft wird eine Wechselwirkungskraft in der Kontaktzone zwischen zwei Körpern[1] oder eine Schnittkraft[2] in einem stabförmigen Bauteil bezeichnet. Sie steht senkrecht zur Kontaktfläche bzw. Schnittfläche. Die in Richtung des Normalenvektors wirkende Normalkraft erzeugt Druck- bzw. Zugspannungen. Die Normalkraft bestimmt u. a. die Reibungskraft zwischen zwei Körpern.
Die Formel zur Berechnung der Normalkraft ergibt sich im Beispiel aus dem Kräftegleichgewicht für den Klotz in Normalenrichtung:
mit
Darin sind enthalten:
- der Kosinus des Winkels der schiefen Ebene
- die Gewichtskraft
- die Masse
- die Schwerebeschleunigung .
Neben dem beschriebenen Fall einer Belastung rein durch das Gewicht treten Normalkräfte z. B. auch als Folge aerodynamischen Abtriebs oder durch den Kurvendruck beim Befahren einer überhöhten Kurve auf. Im letzteren Fall ergibt sich die Normalkraft zu:
mit der Fliehkraft , die horizontal nach außen wirkt.
Balkentheorie
In der Stabtheorie 1. Ordnung ist die Normalkraft die Längskraft parallel zur Stabachsenrichtung:
Weblinks
Einzelnachweise
- ↑ Hans Steger: Maschinenbau für Elektrotechniker. Teil 2. Teubner, 1991, ISBN 3-519-06735-8, S. 69. (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Hans Albert Richard, Manuela Sander: Technische Mechanik. Festigkeitslehre. 2. Auflage. Vieweg+Teubner, 2008, ISBN 978-3-8348-0454-9, S. 32. (eingeschränkte Vorschau in der Google-Buchsuche).






















