Kampyle of Eudoxus

Graph of Kampyle of Eudoxus with a = 1

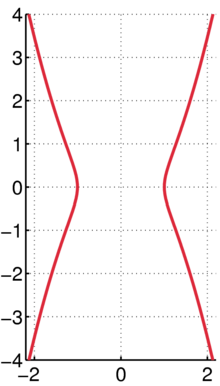
The Kampyle of Eudoxus (Greek: καμπύλη [γραμμή], meaning simply "curved [line], curve") is a curve with a Cartesian equation of

x 4 = a 2 ( x 2 + y 2 ) , {\displaystyle x^{4}=a^{2}(x^{2}+y^{2}),}

from which the solution x = y = 0 is excluded.

Alternative parameterizations

In polar coordinates, the Kampyle has the equation

r = a sec 2 ⁡ θ . {\displaystyle r=a\sec ^{2}\theta .}

Equivalently, it has a parametric representation as

x = a sec ⁡ ( t ) , y = a tan ⁡ ( t ) sec ⁡ ( t ) . {\displaystyle x=a\sec(t),\quad y=a\tan(t)\sec(t).}

History

This quartic curve was studied by the Greek astronomer and mathematician Eudoxus of Cnidus (c. 408 BC – c.347 BC) in relation to the classical problem of doubling the cube.

Properties

The Kampyle is symmetric about both the x- and y-axes. It crosses the x-axis at (±a,0). It has inflection points at

( ± a 6 2 , ± a 3 2 ) {\displaystyle \left(\pm a{\frac {\sqrt {6}}{2}},\pm a{\frac {\sqrt {3}}{2}}\right)}

(four inflections, one in each quadrant). The top half of the curve is asymptotic to x 2 / a − a / 2 {\displaystyle x^{2}/a-a/2} as x → ∞ {\displaystyle x\to \infty } , and in fact can be written as

y = x 2 a 1 − a 2 x 2 = x 2 a − a 2 ∑ n = 0 ∞ C n ( a 2 x ) 2 n , {\displaystyle y={\frac {x^{2}}{a}}{\sqrt {1-{\frac {a^{2}}{x^{2}}}}}={\frac {x^{2}}{a}}-{\frac {a}{2}}\sum _{n=0}^{\infty }C_{n}\left({\frac {a}{2x}}\right)^{2n},}

where

C n = 1 n + 1 ( 2 n n ) {\displaystyle C_{n}={\frac {1}{n+1}}{\binom {2n}{n}}}

is the n {\displaystyle n} th Catalan number.

See also

  • List of curves

References

  • J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 141–142. ISBN 0-486-60288-5.

External links