Binomilause

Alkeisalgebrassa binomilause kuvaa binomin potenssin algebrallisen kehittämisen. Lauseen mukaan on mahdollista kehittää (x + y)ⁿ summaksi, jossa termit ovat muotoa ax^by^c, siten että eksponentit b ja c ovat ei-negatiivisia kokonaislukuja ja b + c = n. Lisäksi jokaisen termin kerroin a on tietty positiivinen kokonaisluku, joka riippuu n:stä ja b:stä. Kun eksponentti on 0, on x tai y jätetty pois kehitelmästä. Esimerkiksi:

${\displaystyle (x+y)^{1}=x+y}$

${\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}}$

${\displaystyle (x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}}$

${\displaystyle (x+y)^{4}=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4}}$

${\displaystyle (x+y)^{5}=x^{5}+5x^{4}y+10x^{3}y^{2}+10x^{2}y^{3}+5xy^{4}+y^{5}}$

Kerroin a termissä x^by^c tunnetaan binomikertoimena ${\displaystyle {\tbinom {n}{b}}}$ tai ${\displaystyle {\tbinom {n}{c}}}$ (näillä kahdella on sama arvo). Nämä kertoimet voidaan laskea kaavasta

${\displaystyle {n \choose b}={\frac {n!}{b!\cdot (n-b)!}}}$

missä b! tarkoittaa luvun b kertomaa.

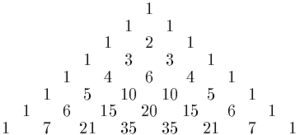
Binomikertoimet voidaan myös järjestää Pascalin kolmioksi. Samat luvut esiintyvät myös kombinatoriikassa, jossa ${\displaystyle {\tbinom {n}{b}}}$ osoittaa, kuinka monta b-alkioista osajoukkoa n alkion joukolla on.

Historiaa

Binomikaava ja kolmion muotoon järjestetyt binomikertoimet liitetään usein vain Blaise Pascaliin, joka kuvaili ne 1600-luvulla, mutta jo monet häntä edeltävät matemaatikot tiesivät ne. 300-luvulla eaa. kreikkalainen matemaatikko Eukleides Aleksandrialainen mainitsi erikoistapauksen binomilauseesta (a+b) eksponentille 2 kuten myös 200-luvun eaa. intialainen matemaatikko Pingala korkeammille kertaluvuille. Tuttu binomilause ja niin kutsuttu Pascalin kolmio olivat tunnettuja 900-luvulla intialaiselle matemaatikolle Halayudhalle ja persialaiselle matemaatikolle Al-Karajille, ja 1200-luvun kiinalaiselle matemaatikolle Yang Huille, jotka kaikki saivat samoja tuloksia. Al-Karaji antoi myös matemaattisen todistuksen sekä binomilauseesta että Pascalin kolmiosta käyttäen matemaattista induktiota.

Lauseen väite

Lauseen mukaan on mahdollista kehittää mikä tahansa potenssi (x + y):n summaksi, joka on muotoa

${\displaystyle (x+y)^{n}={n \choose 0}x^{n}y^{0}+{n \choose 1}x^{n-1}y^{1}+{n \choose 2}x^{n-2}y^{2}+\cdots +{n \choose n-1}x^{1}y^{n-1}+{n \choose n}x^{0}y^{n},}$

missä jokainen ${\displaystyle {\tbinom {n}{k}}}$ on tietty positiivinen kokonaisluku, joka tunnetaan binomikertoimena. Tämä kaava liittyy myös binomikaavaan tai binomikuvaukseen. Käytettäessä summamerkintää se voidaan kirjoittaa

${\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}=\sum _{k=0}^{n}{n \choose k}x^{k}y^{n-k}.}$

Viimeinen lauseke seuraa edellisestä ja on symmetrinen x :n ja y :n ensimmäisen lausekkeen kanssa, ja verrattaessa kertoimiin huomataan, että binomikertoimien jono kaavassa on myös symmetrinen.

Esimerkkejä

Tavallisin esimerkki binomilauseesta on x + y:n neliö:

${\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}.\!}$

Binomikertoimet 1, 2, 1 tässä lausekkeessa vastaavat Pascalin kolmion kolmatta riviä. Korkeampien potenssien kertoimet x + y:lle vastaavat kolmion seuraavia rivejä :

${\displaystyle {\begin{aligned}(x+y)^{3}&=x^{3}+3x^{2}y+3xy^{2}+y^{3},\\[8pt](x+y)^{4}&=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4},\\[8pt](x+y)^{5}&=x^{5}+5x^{4}y+10x^{3}y^{2}+10x^{2}y^{3}+5xy^{4}+y^{5},\\[8pt](x+y)^{6}&=x^{6}+6x^{5}y+15x^{4}y^{2}+20x^{3}y^{3}+15x^{2}y^{4}+6xy^{5}+y^{6},\\[8pt](x+y)^{7}&=x^{7}+7x^{6}y+21x^{5}y^{2}+35x^{4}y^{3}+35x^{3}y^{4}+21x^{2}y^{5}+7xy^{6}+y^{7}.\end{aligned}}}$

Huomaa, että

1. x:n potenssi alenee, kunnes se on 0 (ei yhtään x:ä), alkaen arvosta n ( n potenssissa ${\displaystyle (x+y)^{n}.)}$
2. y:n potenssi kasvaa 0:sta (ei yhtään y:tä), kunnes se on n (myös n potenssissa${\displaystyle (x+y)^{n}.)}$
3. Pascalin kolmion n:s rivi on sama kuin auki kerrotun binomin kertoimet. (Huomaa, että kärki on rivi 0.)

Todistuksia

Kombinatorinen todistus

Esimerkki

xy²n kerroin

${\displaystyle {\begin{aligned}(x+y)^{3}&=(x+y)(x+y)(x+y)\\&=xxx+xxy+xyx+{\underline {xyy}}+yxx+{\underline {yxy}}+{\underline {yyx}}+yyy\\&=x^{3}+3x^{2}y+{\underline {3xy^{2}}}+y^{3}.\end{aligned}}\,}$

on ${\displaystyle {\tbinom {3}{2}}=3}$ koska on kolme kolmen kirjaimen pituista x,y jonoa, joissa on tarkalleen kaksi y'tä, nimittäin,

${\displaystyle xyy,\;yxy,\;yyx,}$

vastaten kolmea kaksialkioista osajoukkoa joukosta { 1, 2, 3 }, nimittäin,

${\displaystyle \{2,3\},\;\{1,3\},\;\{1,2\},}$

missä jokaisessa osajoukossa eritellään yn paikka vastaavassa jonossa.

Yleinen tapaus

Kun kehitetään auki (x + y)ⁿ niin se tuottaa 2 ⁿ tulojen summaa, jotka ovat muotoa e₁e₂ ... e _n missä jokainen e _i on x tai  y. Kun järjestellään termejä uudelleen, niin huomataan, että jokainen tulo on muotoa x^n−ky^k k: n arvoilla 0:sta n:ään. Kun k tunnetaan, saadaan seuraavista kaikista lauseista sama arvo:

• alkioiden lukumäärä x^n − ky^k :n alkioiden kehitelmässä
• n-alkioisten jonojen lukumäärä x:ää ja y:tä, joissa y on tarkalleen k kertaa
• k-alkioisten osajoukkojan lukumäärä joukosta { 1, 2, ..., n}
• ${\displaystyle {n \choose k}}$

Tämä todistaa binomilauseen.

Binomisarja

Jos eksponentti n ei ole positiivinen kokonaisluku eikä nolla, ei lauseketta ${\displaystyle (1+x)^{n}}$ voida kehittää polynomiksi. Yleistetyn binomilauseen mukaan sille on kuitenkin olemassa sarjakehitelmä:

${\displaystyle {\begin{aligned}(1+x)^{\alpha }&=\sum _{k=0}^{\infty }\;{\frac {\alpha (\alpha -1)(\alpha -2)\cdots (\alpha -k+1)}{k!}}x^{k}=1+\alpha x+{\frac {\alpha (\alpha -1)}{2!}}x^{2}+\cdots ,\end{aligned}}}$,

missä yleensä pätee kuitenkin vain, ${\displaystyle |x|<1}$ (ja eräissä tapauksissa silloinkin, kun ${\displaystyle |x|=1}$), jolloin sarja suppenee. Tässä kertoimille ${\displaystyle {\frac {\alpha (\alpha -1)(\alpha -2)\cdots (\alpha -k+1)}{k!}}}$ käytetään myös merkintää ${\displaystyle \alpha \choose k}$. Tätä sarjaa sanotaan binomisarjaksi.

Erikoistapauksessa, kun n on positiivinen kokonaisluku, sarjan kertoimet n+1:nnestä lähtien ovat kaikki nollia, jolloin tuloksena saadaan algebran binomilause.

Lähteet

• Binomial Theorem by Stephen Wolfram, and "Binomial Theorem (Step-by-Step)" by Bruce Colletti and Jeff Bryant, Wolfram Demonstrations Project, 2007.
• Binomial Theorem Introduction (Arkistoitu – Internet Archive)

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Binomilause Wikimedia Commonsissa