Sykloidi

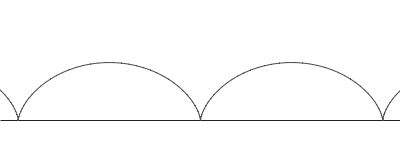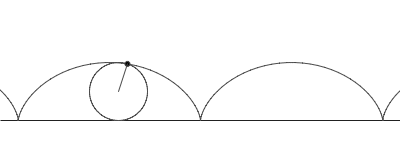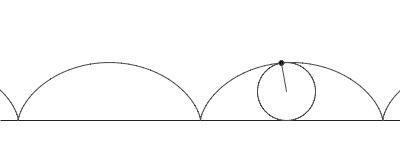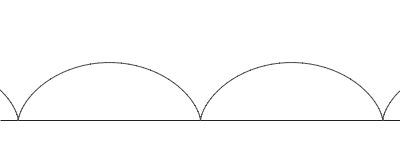
Sykloidi on vierintäkäyrä, jonka muodostavat pyörän pinnalla olevan pisteen sijainnit eri ajanhetkinä, kun pyörä vierii suoraan tasaisella alustalla.

Sykloidi on samalla brakistokroni eli käyrä, jota pitkin kappale nopeimmin vierii huipulta alas painovoiman vaikutuksesta. Samalla se on tautokroni, mikä merkitsee, että aika, jossa sen sisäpintaa pitkin vierivä, alkutilassa lepotilassa jossakin sen pisteessä oleva pallo saavuttaa käyrän alimman kohdan, ei riipu sen alkuperäisestä paikasta.

Historia

Sykloidia tutki ensimmäisenä Nicolaus Cusanus ja myöhemmin Marin Mersenne. Nimen sille antoi Galileo Galilei vuonna 1599. Vuonna 1634 G. P. de Roberval todisti, että sykloidin alle jäävän alueen pinta-ala on kolme kertaa niin suuri kuin sen ympyrän, jonka vieriessä se muodostuu. Vuonna 1658 Christopher Wren osoitti, että sykloidin pituus on neljä kertaa niin suuri kuin sen muodostavan ympyrän läpimitta. Sykloidia on sanottu "Geometrian Helenaksi", ja 1600-luvun matemaatikot kävivät paljon siihen liittyviä kiistoja.

Yhtälöt

Origon kautta kulkeva sykloidi, jonka r-säteinen ympyrä muodostaa vieriessään, muodostuu pisteistä (x, y), jotka toteuttavat ehdot:

${\displaystyle x=r(t-\sin t)\,}$

${\displaystyle y=r(1-\cos t)\,}$

missä parametri t on reaaliluku. Parametrin t arvolla ympyrän keskipiste on pisteessä rt.

Edellä trigonometriset funktiot on määritelty käyttämällä kulmayksikkönä radiaania. Jos kulmayksikkönä käytetään astetta, yhtälöt voidaan kirjoittaa muotoon

x = r(cos(270°-t)) + 2πrt/360°

y = r(sin(270°-t)) + r

Käyrä on derivoituva muualla paitsi erikoispisteissä, joissa se kohtaa x-akselin. Niissä sykloidilla on terävä kärki, ja niitä lähestyttäessä derivaatta kasvaa rajatta ${\displaystyle \infty }$:ään tai ${\displaystyle -\infty }$:ään riippuen siitä, kummasta suunnasta erikoispistettä lähestytään. Sykloidi toteuttaa myös differentiaaliyhtälön

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}={\frac {2r-y}{y}}.}$

Pinta-ala

r-säteisen ympyrän generoiman sykloidin kaari voidaan parametroida näin:

${\displaystyle x=r(t-\sin t),\,}$

${\displaystyle y=r(1-\cos t),\,}$

missä

${\displaystyle 0\leq t\leq 2\pi .\,}$

Koska

${\displaystyle {\frac {dx}{dt}}=r(1-\cos t),}$

on sykloidin kaaren alla olevan alueen pinta-ala

${\displaystyle A=\int _{t=0}^{t=2\pi }y\,dx=\int _{t=0}^{t=2\pi }r^{2}(1-\cos t)^{2}\,dt=\left.r^{2}\left({\frac {3}{2}}t-2\sin t+{\frac {1}{2}}\cos t\sin t\right)\right|_{t=0}^{t=2\pi }=3\pi r^{2}.}$

Kaaren pituus

Sykloidin kaaren pituus S voidaan laskea seuraavasti:

${\displaystyle \int _{0}^{2\pi }\left(\left({\frac {dy}{dt}}\right)^{2}+\left({\frac {dx}{dt}}\right)^{2}\right)^{1/2}\,dt=\int _{0}^{2\pi }2r\sin(t/2)\,dt=8r.}$

Sykloidia muistuttavia käyriä

Episykloidi on käyrä, joka muodostuu ympyrän vieriessä toisen ympyrän kehää pitkin sen ulkopuolella. Hyposykloidi taas muodostuu ympyrän vieriessä toisen ympyrän kehää pitkin sen sisäpuolella. Vastaavasti voidaan muodostaa käyriä ympyrän vieriessä minkä tahansa muutakin käyrää pitkin.

Syklodilla, episykloidilla ja hyposykloidilla on se yhteinen ominausuus, että kukin niistä on yhdenmuotoinen evoluuttansa kanssa.

Lähteet

• An application from physics: Ghatak, A. & Mahadevan, L. Crack street: the cycloidal wake of a cylinder tearing through a sheet. Physical Review Letters, 91, (2003). http://link.aps.org/abstract/PRL/v91/e215507

• D. Wells: The Penguin Dictionary of Curious and Interesting Geometry, s. pp. 445–47. New York: Penguin Books, 1991. 0-14-011813-6. (englanniksi)

Aiheesta muualla

Wikimedia Commonsissa on kuvia tai muita tiedostoja aiheesta Sykloidi.

• Cycloids at cut-the-knot
• Richard A. Proctorin sivusto sykloidista ja sitä muistuttavista käyristä
• Cornell University Library.
• Sykloidit ja trokoidit (Arkistoitu – Internet Archive)
• Cycloid Curves by Sean Madsen with contributions by David von Seggern, The Wolfram Demonstrations Project.