Tasakylkinen kolmio

Tasakylkinen kolmio on sellainen kolmio, jossa kaksi sivua ovat keskenään yhtä pitkät. Englantilainen nimitys tasakylkiselle kolmiolle on isosceles triangle, joka tulee kreikan kielen sanoista iso ('sama, yhtäsuuri') ja skelos ('sääri, jalka').^[1]

Tasakylkisellä kolmiolla yksi sivu on yleensä erimittainen kuin muut sivut. Tätä kutsutaan kannaksi.^[2] Kannan pituus on pisimmillään lähes kaksi kertaa kyljen pituus. Tasakylkisiä kolmioita kohdataan usein sovelluksissa, jossa ihmisen rakennelma on pystytetty symmetrisesti. Nimitys "kanta" lienee käytännöllistä perua. Esimerkiksi niin sanotut A-tikkaiden muoto on tasakylkinen kolmio, jossa kanta on luonnollisella tavalla kolmion alin sivu.

Jos kanta on samanpituinen kuin kylki, on kyseessä tasasivuinen kolmio.

Tasakylkisessä kolmiossa on kaksi yhtäpitkää sivua, joita kutsutaan kyljiksi.^[2] Kyljen pituus on lyhimmillään hieman pitempi kuin kannan puolikas, mutta se voi olla kuinka pitkä hyvänsä. Samoin kuin johdettiin nimitys "kanta", voidaan sana "kylki" johtaa käytännön tilanteista, jossa tasakylkinen kolmio on "kannallaan" ja "kyljet" ovat kolmion sivuilla.

Kantakulma muodostuu kannan ja toisen kyljen väliin. Tasakylkisessä kolmiossa kantakulmat ovat samansuuruisia.^[2][3][4] Se on suuruudeltaan aina alle 90°. Jos se on

• 45°, on kyseessä suorakulmainen tasakylkinen kolmio
• 60°, on kyseessä tasasivuinen kolmio

• 
  Suorakulmaisen tasakylkisen kolmion kantakulma on 45°.
• 
  Tasasivuisessa kolmiossa on kantakulma 60°.

Kannan vastaista kärkeä kutsutaan huipuksi. Huippukulma muodostuu huippuun kylkien väliin.^[2] Se on suuruudeltaan aina alle 180° ja se voidaan laskea kantakulman avulla ${\displaystyle \alpha =180^{\circ }-2\beta }$. Jos huippukulma on

• 60°, on kyseessä tasasivuinen kolmio.
• 90°, on kyseessä suorakulmainen tasasivuinen kolmio.
• alle 90°, on se teräväkulmainen tasasivuinen kolmio.
• yli 90°, on kyseessä tylppäkulmainen tasasivuinen kolmio.

• 
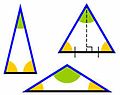  Huippukulma on aina alle 180° astetta.
• 
  Huippu on alle 90°, jolloin kolmio on teräväkulmainen tasasivuinen kolmio.
• 
  Huippu, tässä vasen kulma, on 90°, jolloin kolmio on suorakulmainen tasakylkinen kolmio.
• 
  Huippu, tässä vasen kulma, on yli 90°, jolloin kolmio on tylppä tasasivuinen kolmio.

Tasakylkisessä kolmiossa kantakulmat ovat yhtä suuret. Tämä nähdään seuraavalla päättelyllä, jossa hyödynnetään yleisen kolmion kulmien summan ominaisuutta: ${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$ ^[5]. Taitetaan ensin tasakylkinen kolmio kahtia niin, että yhtä pitkät kyljet yhtyvät. Silloin taitekohta muodostaa janan kolmion huipusta sen kannalle. Koska kyljet yhtyvät, jakaa taitos huippukulman kahteen yhtäsuureen kulmaan ${\displaystyle (\alpha =\alpha ')}$. Kantakulmat yhtyvät myös, koska kanta on suora, ja siksi nekin ovat yhtäsuuret ${\displaystyle (\beta =\beta ')}$ ja näin on molemmissa puoliskoissa kaksi vastinkulmaparia yhtä suuret. Näillä perusteluilla todetaan tasakylkisen kolmion kantakulmat yhtäsuuriksi ja taitoksen synnyttämän janan olevan huipun kulmanpuolittaja.^[2]

Huipun kulmanpuolittajalla on muitakin ominaisuuksia. Kummankin kolmion kolmas kulma voidaan laskea ja todeta yhtäsuureksi

${\displaystyle \gamma =180^{\circ }-\alpha -\beta =180^{\circ }-\alpha '-\beta '=\gamma '.}$

Koska ${\displaystyle \gamma }$ ja ${\displaystyle \gamma '}$ ovat oikokulman vieruskulmia ja yhtäsuuret, ovat ne 90°. Koska taitoksen jana kulkee huipun kautta ja on kohtisuorassa kantaa vasten, todetaan se myös korkeusjanaksi. Se on myös kannan sivunpuolittaja eli mediaani, sillä taitos jakaa tasasivuisen kolmion yhteneviksi kolmioiksi, joilla on myös yhtäpitkät vastinsivut. Silloin myös kannan puoliskot ovat yhtä pitkät. Kohtisuoruuden vuoksi sivunpuolittajaa voi pitää myös keskinormaalina.^[2]

Merkitään seuraavissa yhtälöissä kolmion osat seuraavasti:

• Kolmion sivut: kanta merkitään ${\displaystyle a}$ ja kyljet ${\displaystyle b}$.
• Kolmion kulmat: huippukulma meritään ${\displaystyle \alpha }$ ja kantakulmat ${\displaystyle \beta }$
• Korkeusjanat: kantaa vastaan ${\displaystyle h_{a}}$ ja kylkeä vastaan ${\displaystyle h_{b}}$.
• Kolmion piirin pituuden puolikas on ${\displaystyle s={\tfrac {1}{2}}(a+b+b)={\tfrac {1}{2}}(a+2b)}$.

Silloin voidaan esittää tasakylkisen kolmion ominauuksia seuraavasti.

• Kolmion kantaa vastaava korkeus on ${\displaystyle h=h_{a}={\sqrt {b^{2}-{\tfrac {1}{4}}a^{2}}}}$.^[1]
• Kolmion kylkeä vastaava korkeus on ${\displaystyle h_{b}={\frac {2A}{b}}={\frac {a{\sqrt {b^{2}-{\tfrac {1}{4}}a^{2}}}}{b}}}$

Heronin pinta-alan kaavasta voidaan johtaa korkeusjanoille toiset yhtälöt.

• ${\displaystyle h_{a}={\frac {2A}{a}}={\frac {2{\sqrt {s(s-a)(s-b)^{2}}}}{a}}}$
• ${\displaystyle h_{b}={\frac {2A}{b}}={\frac {2{\sqrt {s(s-a)(s-b)^{2}}}}{b}}}$
• Kolmion pinta-ala on ${\displaystyle A={\frac {1}{2}}ah_{a}={\frac {1}{2}}bh_{b}={\tfrac {1}{2}}a^{2}{\sqrt {{\tfrac {b^{2}}{a^{2}}}-{1}{4}}}={\sqrt {p(p-a)(s-b)^{2}}}}$.^[1]
• Jos huippukulma on ${\displaystyle \alpha }$, niin ala on ${\displaystyle A={\tfrac {1}{2}}b^{2}\sin {{\tfrac {1}{2}}\alpha }.}$^[1]

Tasakylkisen kolmion sisään piirretyn ympyrän säde on ${\displaystyle r={\frac {a({\sqrt {a^{2}+4h^{2}}}-a)}{4h}}.}$ Jos kolmio on suorakulmainen tasakylkinen kolmio, on säde ${\displaystyle r=a(1-{\tfrac {1}{2}}{\sqrt {2}}).}$ ^[6]

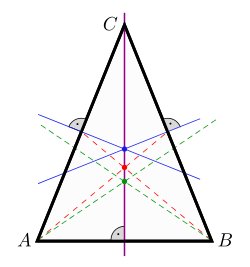
Kylkien korkeusjanat leikkaavat toisensa huipun halkaisijalla pisteessä, joka on kolmion ortokeskus.^[7][8]

Kantakulmien puolittajat kohtaavat kolmion halkaisijalla pisteessä, joka on kolmion sisään piirretyn ympyrän keskipiste. Keskipiste on yksi kolmion merkillisistä pisteistä. Keskipiste jakaa halkaisijan suhteessa 2 : 1 siten, että lyhyempi osa jää kolmion kannan puolelle.^[9]

Kolmion kylkien keskinormaalit leikkaavat kolmion huipun halkaisijalla pisteessä, joka on kolmion ympäri piirretyn ympyrän keskipiste. Myös tämä piste on kolmion merkillisiä pisteitä.^[10]

Kylkien keskijanat leikkaavat kolmion huipun halkaisjalla pisteessä, joka on kolmion painopiste.^[9]

Huipun puolittaja jakaa tasakylkisen kolmion kahdeksi yhteneväksi suorakulmaiseksi kolmioksi. Kaikki tasakylkisen kolmion merkilliset pisteet sijaitsevat symmetrisesti kolmion halkaisevalla janalla. Koska neljä edellistä pistettä ovat halkaisijalla, on se samalla osa Eulerin suoraa.^[7][11]

Jos kolmion kaksi kulmanpuolittajaa ovat yhtäpitkät, on kolmio tasakylkinen kolmio.^[12]

• Väisälä Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
• Kurittu Lassi: Geometria (pdf) (luentomoniste) 2006. Jyväskylän: Jyväskylän Yliopisto.