Négyzetgyök 2

Az egységnyi oldalú egyenlő szárú derékszögű háromszög átfogójának hossza négyzetgyök 2

A négyzetgyök kettő, más néven Püthagorasz-állandó, ami felírva:

2 {\displaystyle {\sqrt {2}}}

vagy törtkitevős hatványként

2 1 2 {\displaystyle 2^{\frac {1}{2}}}

egy pozitív, valós szám, melyet önmagával szorozva 2-t kapunk. Az első 65 tizedesjegye a következő (A002193 sorozat az OEIS-ben):

1,41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799.

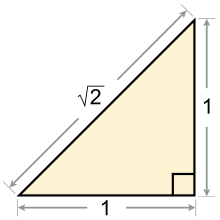
A √2 valószínűleg az elsőként megismert irracionális szám. A geometriai jelentősége az, hogy ez a hossza az egységnyi oldalú négyzet átlójának, illetve egy egységnyi oldalú kocka lapátlójának, ami levezethető a Pitagorasz-tételből.

Irracionális számok
2 {\displaystyle {\sqrt {2}}}
Bináris 1,0110101000001001111…
Decimális 1,4142135623730950488…
Hexadecimális 1,6A09E667F3BCC908B2F…
Lánctörtes alakban 1 + 1 2 + 1 2 + 1 2 + 1 ⋱ {\displaystyle 1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{\ddots }}}}}}}}}

Az ezüstmetszés arányszáma

1 + 2 . {\displaystyle 1+{\sqrt {2}}.\,}

Történet

Az YBC 7289-es babiloni agyagtábla jegyzetekkel

A Yale Egyetem babiloni gyűjteményében található 7289-es számú agyagtábla (i. e. 1800-1600-ból) már közelítő értéket ad a 2 {\displaystyle {\sqrt {2}}} -re a babiloniak által használt hatvanas számrendszerben, hat tizedesjegy pontossággal:

1 + 24 60 + 51 60 2 + 10 60 3 = 1 , 41421 296 ¯ . {\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1,41421{\overline {296}}.}

Ennek a számnak egy másik korai közelítését az ősi indiai matematikai szövegek adják, a következőképp: Növeljük az oldal hosszát a harmadával, azután a harmadának a negyedével, majd csökkentsük a negyedének a harmincnegyedével. Tehát:

1 + 1 3 + 1 3 ⋅ 4 − 1 3 ⋅ 4 ⋅ 34 = 577 408 ≈ 1 , 414215686. {\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1,414215686.}

Az irracionális számok felfedezését általában Püthagorasz egyik tanítványának, a metapontumi Hippaszosznak tulajdonítják, aki elkészítette az első (valószínűleg geometriai) bizonyítást a gyök 2 irracionalitására. Egy legenda szerint Pitagorasz hitt a számok teljességében, és nem tudta elfogadni az irracionális számok létezését. Nem tudta megcáfolni a létezésüket logikai úton, de a hite miatt nem tudta elfogadni irracionális számok létezését, ezért fulladásos halálra ítélte Hippaszoszt. Más legendák szerint Hippaszoszt megfojtotta Pitagorasz néhány tanítványa, vagy csupán kizárták a körükből.

Kiszámítási algoritmus

Számos módszer van a √2 közelítő értékének számolására, melyek a kifejezéseket egész számok arányaként, vagy tizedestörtként közelítik meg. Erre a legegyszerűbb algoritmus, amely sok számítógép és számológép alapja, a babiloni módszer a négyzetgyök számolására. Ez a következőképp működik:

Először vegyünk egy tetszőleges becslést. A becslés pontossága nem számít, csak azt befolyásolja, hányszor kell megismételni a lépéseket, hogy elérjünk egy bizonyos pontosságú közelítést. Ezután használhatjuk a becslésünket a következő rekurzív számításban:

F n + 1 = F n + 2 F n 2 . {\displaystyle F_{n+1}={\frac {F_{n}+{\frac {2}{F_{n}}}}{2}}.}

Minél több ismétlés van az algoritmusban (egyre több számolást kell elvégezni, egyre nagyobb n-nel), annál jobb becslést kapunk a √2 közelítő értékére.

1997-ben Kanada Jaszumasza csapatával 137 438 953 444 tizedesjegyig számolta ki a √2 közelítő értékét.

2006 februárjában a rekordot túlszárnyalták egy otthoni számítógépen. Kondó Sigeru az első 200 000 000 000 tizedesjegyét számolta ki a √2-nek, alig 13 nap és 14 óra kellett hozzá egy 3,6 GHz-es PC-vel, 16 GB memóriával.

Irracionalitásának bizonyítása

Indirekt bizonyítás

Az indirekt bizonyítás azt jelenti, hogy feltesszük, hogy az állításunk tagadása igaz, majd átalakításokkal nyilvánvaló ellentmondást kapunk, tehát a tagadás hamis, ezért az eredeti állítás igaz.

  1. Tegyük fel, hogy a 2 {\displaystyle {\sqrt {2}}} egy racionális szám, tehát léteznek a {\displaystyle a} és b {\displaystyle b} egészek, hogy a b = 2 {\displaystyle {\frac {a}{b}}={\sqrt {2}}} .
  2. Akkor lehet felírni 2 {\displaystyle {\sqrt {2}}} -t tovább nem egyszerűsíthető törtként, ha a {\displaystyle a} és b {\displaystyle b} relatív prímek, valamint ( a b ) 2 = 2 {\displaystyle \left({\frac {a}{b}}\right)^{2}=2} .
  3. Ebből következik, hogy a 2 b 2 = 2 {\displaystyle {\frac {a^{2}}{b^{2}}}=2} és a² = 2 b². ((a / b)n = an / bn)
  4. Tehát, a² páros, mert egyenlő 2 b²-tel.
  5. Ebből következik, hogy a is páros, mert csak a páros számoknak páros a négyzetük.
  6. Mivel a páros, létezik k egész szám, ami teljesíti, hogy a = 2k.
  7. Behelyettesítve 2k-t a (6). lépésből a (3). lépés második egyenlőségébe: 2b² = (2k)², ami megegyezik 2b² = 4k², ami megegyezik b² = 2k².
  8. Mivel 2k² osztható 2-vel, és 2k² = b², ezért b² szintén osztható 2-vel, tehát b is.
  9. Az (5). és (8). lépésből tudjuk, hogy a és b is párosak, ami ellentmond annak, hogy relatív prímek, ahogy azt megállapítottuk a (2). lépésben.
Q. E. D.

Mivel van ellentmondás, az (1)-es feltétel, hogy a 2 {\displaystyle {\sqrt {2}}} racionális szám, hamis. Az állítás be van bizonyítva: 2 {\displaystyle {\sqrt {2}}} irracionális.

Ennek a bizonyításnak az általánosításával bármelyik természetes szám négyzetgyökéről el tudjuk dönteni, hogy racionális vagy irracionális.

Bizonyítás végtelen leszállással

Lásd itt: Végtelen leszállás#Példák

Bizonyítás prímtényezős felbontással

Ez a bizonyítás hasonló az előzőhöz, de a számelmélet alaptételét alkalmazza:

  1. Tegyük fel, hogy a 2 {\displaystyle {\sqrt {2}}} egy racionális szám, tehát léteznek a {\displaystyle a} és b {\displaystyle b} egészek, hogy a b = 2 {\displaystyle {\frac {a}{b}}={\sqrt {2}}} .
  2. Ebből következik, hogy a 2 b 2 = 2 {\displaystyle {\frac {a^{2}}{b^{2}}}=2} és a 2 = 2 b 2 {\displaystyle a^{2}=2b^{2}} .
  3. A számelmélet alaptételéből következik, hogy a-nak és b-nek egyértelműen létezik prímtényezős felbontása, amit fel lehet írni a = 2xk és b = 2ym alakban, ahol x és y nemnegatív egészek, m és k pedig páratlan nemnegatív egészek.
  4. Tehát a² = 22xk² és b² = 22ym².
  5. Ha ezt behelyettesítjük a (3). lépésbe, akkor azt kapjuk, hogy 22xk² = 2·22ym² = 22y+1m².
  6. Tehát azt állítjuk, hogy egy prímtényezős felbontás, amelyben 2 páros kitevőjű hatványa van (a kitevő 2x) megegyezik egy olyannal, amelyben a 2 páratlan kitevőjű hatványa szerepel (a kitevő 2y+1). Ez ellentmond az egyértelmű prímfelbontásnak, tehát az indirekt feltevés hamis volt.

Egy másik bizonyítás

A következő reductio ad absurdum egy kevésbé jól ismert bizonyítása a 2 {\displaystyle {\sqrt {2}}} irracionalitásának. Azt a további információt használja, hogy 2 > 1 {\displaystyle {\sqrt {2}}>1} .

  1. Tegyük fel, hogy 2 {\displaystyle {\sqrt {2}}} racionális szám, tehát léteznek m és n egészek, ahol n ≠ 0, hogy m n = 2 {\displaystyle {\frac {m}{n}}={\sqrt {2}}} .
  2. Tehát √2-t fel lehet írni m n {\displaystyle {\frac {m}{n}}} tovább nem egyszerűsíthető törtként, ahol m és n pozitív egészek, mert m n = 2 {\displaystyle {\frac {m}{n}}={\sqrt {2}}} .
  3. 2 = 2 ⋅ n ( 2 − 1 ) n ( 2 − 1 ) = 2 n − 2 n 2 n − n = 2 n − m m − n ,  mivel  2 n = m . {\displaystyle {\sqrt {2}}={\frac {{\sqrt {2}}\cdot n({\sqrt {2}}-1)}{n({\sqrt {2}}-1)}}={\frac {2n-{\sqrt {2}}n}{{\sqrt {2}}n-n}}={\frac {2n-m}{m-n}},{\text{ mivel }}{\sqrt {2}}\,n\,=\,m.}
  4. 2 > 1 {\displaystyle {\sqrt {2}}>1} , ebből következik, hogy m > n, tehát m > 2n – m.
  5. Tehát az m n {\displaystyle {\frac {m}{n}}} törtet, amiről a (2). lépésből tudjuk, hogy nem lehet tovább egyszerűsíteni, a (3). lépésben egyszerűsítjük. Ez ellentmondás, tehát az állítás, hogy a 2 {\displaystyle {\sqrt {2}}} racionális, hamis.

Geometriai bizonyítás

(A kép adatai)
(A kép adatai)

Ez szintén egy példa a végtelen leszállással történő bizonyításra. Alkalmazzuk benne a klasszikus szerkesztést, a tétel bizonyításának ez a módja egyszerűbb, mint amit az ókori görögök alkalmaztak.

Legyen ABC egy egyenlő szárú derékszögű háromszög, az átfogó hossza m, a befogóké n. A Pitagorasz-tétel miatt m/n = √2. Tegyük fel, hogy m és n egész számok. Legyen az m:n arány egyszerűsítve.

Rajzoljunk A középpontú m és n sugarú köríveket. A kapott metszéspontok a szárakon D és E. Ebből következik, hogy AB = AD, AC = AE és ∠BAC and ∠DAE szögek egybevágóak. Tehát az ABC és ADE háromszögek egybevágóak, mert megegyezik 2 oldaluk és az általuk közbezárt szög.

Mivel ∠EBF szög derékszög, és ∠BEF pedig a derékszög fele (45°) BEF szintén egyenlő szárú derékszögű háromszög. Ezért BE = m ‒ n, tehát BF = m ‒ n. A szimmetria miatt DF = m ‒ n, és FDC szintén egyenlő szárú derékszögű háromszög. Ebből következik: FC = n ‒ (m ‒ n) = 2n ‒ m.

Tehát van egy kisebb egyenlő szárú derékszögű háromszögünk, átfogójának hossza 2n ‒ m, a befogóké pedig m ‒ n. Ezek az értékek szintén egészek, arányuk megegyezik m és n arányával, ez ellentmond annak az állításnak, hogy m:n egyszerűsítve van. m és n tehát nem lehetnek egészek, ezért √2 irracionális.

A négyzetgyök 2 tulajdonságai

A gyök 2 fele, ami közelítve 0.70710 67811 86548, egy közös mennyisége a geometriának és a trigonometriának, mert ha az egységvektor a síkon 45°-os szöget zár be a tengelyekkel, akkor a koordinátái:

( 2 2 , 2 2 ) . {\displaystyle \left({\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right).}

És ez kielégíti, hogy

2 2 = 1 2 = 1 2 = cos ⁡ ( 45 ∘ ) = sin ⁡ ( 45 ∘ ) . {\displaystyle {\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos(45^{\circ })=\sin(45^{\circ }).}

Egy érdekes tulajdonsága a négyzetgyök kettőnek a következő:

  1 2 − 1 = 2 + 1. {\displaystyle \!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1.}

Ez az ezüstmetszés egyik tulajdonságának a következménye.

Másik érdekes tulajdonsága a négyzetgyök kettőnek:

2 + 2 + 2 ⋯ = 2 {\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2}}\cdots }}}}=2}

A négyzetgyök 2 kifejezhető az i képzetes egység segítségével, a négyzetgyökvonást, és a számtani műveleteket használva:

i + i i i {\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}} és − i − i − i − i . {\displaystyle {\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}.}

Előállítás sorokkal és produktummal

A cos ⁡ ( π 4 ) = sin ⁡ ( π 4 ) = 1 2 {\displaystyle \cos \left({\frac {\pi }{4}}\right)=\sin \left({\frac {\pi }{4}}\right)={\frac {1}{\sqrt {2}}}} azonosság, és a szinusz és koszinusz végtelen szorzatként való előállításából következnek az alábbi egyenletek:

1 2 = ∏ k = 0 ∞ ( 1 − 1 ( 4 k + 2 ) 2 ) = ( 1 − 1 4 ) ( 1 − 1 36 ) ( 1 − 1 100 ) ⋯ {\displaystyle {\frac {1}{\sqrt {2}}}=\prod _{k=0}^{\infty }\left(1-{\frac {1}{(4k+2)^{2}}}\right)=\left(1-{\frac {1}{4}}\right)\left(1-{\frac {1}{36}}\right)\left(1-{\frac {1}{100}}\right)\cdots }

és

2 = ∏ k = 0 ∞ ( 4 k + 2 ) 2 ( 4 k + 1 ) ( 4 k + 3 ) = ( 2 ⋅ 2 1 ⋅ 3 ) ( 6 ⋅ 6 5 ⋅ 7 ) ( 10 ⋅ 10 9 ⋅ 11 ) ( 14 ⋅ 14 13 ⋅ 15 ) ⋯ {\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }{\frac {(4k+2)^{2}}{(4k+1)(4k+3)}}=\left({\frac {2\cdot 2}{1\cdot 3}}\right)\left({\frac {6\cdot 6}{5\cdot 7}}\right)\left({\frac {10\cdot 10}{9\cdot 11}}\right)\left({\frac {14\cdot 14}{13\cdot 15}}\right)\cdots }

vagy ezzel ekvivalens,

2 = ∏ k = 0 ∞ ( 1 + 1 4 k + 1 ) ( 1 − 1 4 k + 3 ) = ( 1 + 1 1 ) ( 1 − 1 3 ) ( 1 + 1 5 ) ( 1 − 1 7 ) ⋯ . {\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }\left(1+{\frac {1}{4k+1}}\right)\left(1-{\frac {1}{4k+3}}\right)=\left(1+{\frac {1}{1}}\right)\left(1-{\frac {1}{3}}\right)\left(1+{\frac {1}{5}}\right)\left(1-{\frac {1}{7}}\right)\cdots .}

A szám kifejezhető trigonometrikus függvények Taylor-sor alakban történő felírásával. Például cos(π/4) sora adja a következőt:

1 2 = ∑ k = 0 ∞ ( − 1 ) k ( π 4 ) 2 k ( 2 k ) ! . {\displaystyle {\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k}}{(2k)!}}.}

A 1 + x {\displaystyle {\sqrt {1+x}}} Taylor-sora x = 1 esetben a következő:

2 = ∑ k = 0 ∞ ( − 1 ) k + 1 ( 2 k − 3 ) ! ! ( 2 k ) ! ! = 1 + 1 2 − 1 2 ⋅ 4 + 1 ⋅ 3 2 ⋅ 4 ⋅ 6 − 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ⋅ 8 + ⋯ . {\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }(-1)^{k+1}{\frac {(2k-3)!!}{(2k)!!}}=1+{\frac {1}{2}}-{\frac {1}{2\cdot 4}}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6\cdot 8}}+\cdots .}

A sorok konvergenciája gyorsítható Euler-transzformációval, előállítva

2 = ∑ k = 0 ∞ ( 2 k + 1 ) ! ( k ! ) 2 2 3 k + 1 = 1 2 + 3 8 + 15 64 + 35 256 + 315 4096 + 693 16384 + ⋯ . {\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }{\frac {(2k+1)!}{(k!)^{2}2^{3k+1}}}={\frac {1}{2}}+{\frac {3}{8}}+{\frac {15}{64}}+{\frac {35}{256}}+{\frac {315}{4096}}+{\frac {693}{16384}}+\cdots .}

Előállítása lánctörttel

A négyzetgyök 2 a következő lánctörtként áll elő:

  2 = 1 + 1 2 + 1 2 + 1 2 + 1 ⋱ . {\displaystyle \!\ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{\ddots }}}}}}}}.}

A papír mérete

Gyök 2 kerekített értéke a papír oldalainak aránya az ISO 216-os szabványban. Ez az arány biztosítja, hogy ha félbevágunk egy lapot a rövidebb oldallal párhuzamosan, akkor a kapott papírok oldalainak aránya megegyezik az eredeti papír oldalainak arányával. Valóban, ha egy téglalap oldalai x {\displaystyle x} és x 2 {\displaystyle x{\sqrt {2}}} , akkor a felének az oldalai x {\displaystyle x} és x 2 / 2 {\displaystyle x{\sqrt {2}}/2} , az utóbbi megegyezik x / 2 {\displaystyle x/{\sqrt {2}}} -vel. Ennek következtében, a hosszú oldal ( x {\displaystyle x} ) és a rövid oldal ( x / 2 {\displaystyle x/{\sqrt {2}}} ) aránya ismét 2 {\displaystyle {\sqrt {2}}} .

Kapcsolódó szócikkek

Külső hivatkozások

  • √2.net Archiválva 2021. június 30-i dátummal a Wayback Machine-ben, valós idejű számolás
  • A négyzetgyök 2 első 5 millió számjegye (Jerry Bonnell és Robert Nemiroff, 1994.)
  • A négyzetgyök 2 irracionális, bizonyítások gyűjteménye

Források

  • Apostol, Tom M. (2000. November). „Irrationality of The Square Root of Two — A Geometric Proof”. The American Mathematical Monthly 107 (9), 841–842. o. DOI:10.2307/2695741.  
  • Flannery, David. The Square Root of Two. Springer (2005). ISBN 0-387-20220-X 
  • Fowler, David, Eleanor Robson (1998. November). „Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context”. Historia Mathematica 25 (4), 366–378. o. [2006. szeptember 3-i dátummal az eredetiből archiválva]. DOI:10.1006/hmat.1998.2209.  
  • Gourdon, X. & Sebah, P. Pythagoras' Constant: √2. Includes information on how to compute digits of 2 {\displaystyle {\sqrt {2}}} .
  • Henderson, David W., Square Roots in the Sulbasutra
  • Weisstein, Eric W.: Pythagoras's Constant (angol nyelven). Wolfram MathWorld