Teorema di Menelao

Il teorema di Menelao è un noto teorema in geometria elementare, attribuito al matematico Menelao di Alessandria, che tratta dei triangoli nella geometria piana.

Dati un triangolo di vertici A, B, C e tre punti D, E ed F che giacciono rispettivamente sulle rette BC, AC e AB, D, E ed F sono allineati se e solo se:

${\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1.}$^[1]

In questa equazione, ${\displaystyle AF}$, ${\displaystyle FB}$, ecc., rappresentano la misura dei segmenti considerati con segno. Per esempio, la frazione ${\displaystyle AF/FB}$ ha segno positivo solo quando la retta per ${\displaystyle D}$, ${\displaystyle E}$ ed ${\displaystyle F}$ interseca il lato ${\displaystyle AB}$.

Si tiene anche conto dell'orientamento dei segmenti, cioè:

${\displaystyle AB=-BA}$

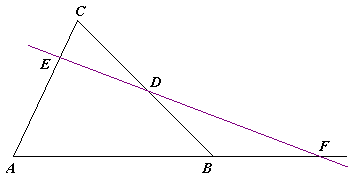
Si osserva che il membro a sinistra dell'equazione ha segno negativo se tutti e tre i rapporti sono negativi, caso in cui la retta ${\displaystyle DEF}$ non interseca il triangolo, oppure un rapporto è negativo e gli altri due positivi, caso in cui la retta ${\displaystyle DEF}$ interseca il triangolo in due punti (si veda l'assioma di Pasch).

Si costruiscano le perpendicolari da ${\displaystyle A}$, ${\displaystyle B}$ e ${\displaystyle C}$ su ${\displaystyle DEF}$, le chiamo rispettivamente ${\displaystyle a}$,${\displaystyle b}$ e ${\displaystyle c}$. Ora per similitudine di triangoli, segue che:

${\displaystyle \left|{\frac {AF}{FB}}\right|=\left|{\frac {a}{b}}\right|\ ,\ \left|{\frac {BD}{DC}}\right|=\left|{\frac {b}{c}}\right|\ ,\ \left|{\frac {CE}{EA}}\right|=\left|{\frac {c}{a}}\right|}$

Cioè:

${\displaystyle \left|{\frac {AF}{FB}}\right|\cdot \left|{\frac {BD}{DC}}\right|\cdot \left|{\frac {CE}{EA}}\right|=\left|{\frac {a}{b}}\cdot {\frac {b}{c}}\cdot {\frac {c}{a}}\right|=1}$

Dove l'ultima uguaglianza si è ottenuta semplificando le frazioni all'interno del modulo.

Per l'altro verso dell'implicazione:

siano ${\displaystyle D,\ E}$ ed ${\displaystyle F}$ appartenenti rispettivamente alle rette ${\displaystyle BC,\ AC}$ e ${\displaystyle AB}$, in modo che l'equazione valga. Sia ${\displaystyle F'}$ il punto in cui le rette ${\displaystyle DE}$ e ${\displaystyle AB}$ si intersecano. Allora per quanto dimostrato in precedenza anche ${\displaystyle D,\ E}$ ed ${\displaystyle F'}$ verificano l'equazione. Confrontandole:

${\displaystyle {\frac {AF}{FB}}={\frac {AF'}{F'B}}}$

Ma al più un punto può spezzare un segmento in due con un dato rapporto, quindi si conclude che:

${\displaystyle F=F'.}$

• Assioma di Pasch
• Teorema di Ceva

• Wikimedia Commons contiene immagini o altri file su teorema di Menelao

• (EN) Menelaus’ theorem, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Teorema di Menelao, su MathWorld, Wolfram Research.
• (EN) Branko Grünbaum, G. C. Shepard, Ceva, Menelaus, and the Area Principle (PDF), in Mathematical Magazine, vol. 68, Mathematical Association of America, ottobre 1995, 254-268.
• Giuseppe Peano, Calcolo geometrico secondo l'Ausdehnungslhere di H. Grassmann, Fratelli Bocca Editori, 1888, pp. 44-48. http://mathematica.sns.it/opere/138/

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica