サイクロイド(英語: cycloid)とは、円がある規則にしたがって回転するときの円上の定点が描く軌跡として得られる平面曲線の総称である。一般にサイクロイドといえば定直線上を回転するものを指すことが多い。擺線(はいせん)とも呼ばれる。サイクロイドと併せて外サイクロイドや内サイクロイドについても解説する。
定義および性質
定直線に沿って円が滑らずに回転するときの円周上の定点の軌跡をサイクロイドという(→生成アニメーション)。サイクロイドはトロコイドの一種と見なすことができる。半アーチ分の伸開線は、自身と合同なサイクロイドとなる。逆に言うと、サイクロイドの縮閉線は、自身と合同なサイクロイドとなる。
動円の半径を rm, 回転角を θ とすると、サイクロイドの媒介変数表示は



 サイクロイドの半アーチ分の伸開線。半アーチ分の弧長は、動円半径の4倍となる。
サイクロイドの半アーチ分の伸開線。半アーチ分の弧長は、動円半径の4倍となる。 - "円が1回転したときの定点の軌跡" の長さを l とすると、

 サイクロイドの面積をマミコンの定理(英語版)により求める図。サイクロイドを囲む長方形(面積 2rm × 2πrm = 4πrm2)からサイクロイド自身を取り除いた領域の面積は、動円の面積 πrm2 に等しい。
サイクロイドの面積をマミコンの定理(英語版)により求める図。サイクロイドを囲む長方形(面積 2rm × 2πrm = 4πrm2)からサイクロイド自身を取り除いた領域の面積は、動円の面積 πrm2 に等しい。 - "円が1回転したときの定点の軌跡" と "x-軸" で囲まれた部分の面積を S とすると、




応用分野
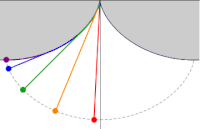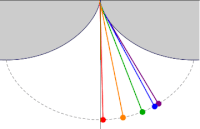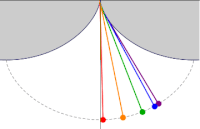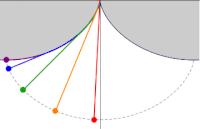 振幅の異なる5つのサイクロイド振り子。おもりの軌跡はサイクロイドとなる。
振幅の異なる5つのサイクロイド振り子。おもりの軌跡はサイクロイドとなる。 参考文献
- Apostol, Tom M.、Mnatsakanian, Mamikon A. 著、川辺治之 訳『Aha! ひらめきの幾何学―アルキメデスも驚くマミコンの定理―』共立出版、2016年8月。ISBN 978-4-320-11138-7。
関連項目
外部リンク
- 『サイクロイド』 - コトバンク
- Weisstein, Eric W. "Cycloid". mathworld.wolfram.com (英語).
- Cycloids at cut-the-knot
- A Treatise on The Cycloid and all forms of Cycloidal Curves, monograph by Richard A. Proctor, B.A. posted by Cornell University Library.
- “Cicloides y Trocoides”. 2009年12月12日時点のオリジナルよりアーカイブ。2017年7月8日閲覧。
- Cycloid Curves by Sean Madsen with contributions by David von Seggern, en:Wolfram Demonstrations Project.
典拠管理データベース: 国立図書館  | |
|---|
 サイクロイドの図示
サイクロイドの図示 サイクロイド (rm = 1, −π ≤ θ ≤ 3π)
サイクロイド (rm = 1, −π ≤ θ ≤ 3π)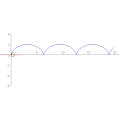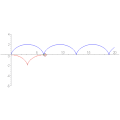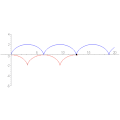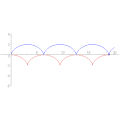 サイクロイドの縮閉線。
サイクロイドの縮閉線。




















