Pavare trihexagonală romboidală
| Pavare trihexagonală romboidală | |
 | |
| Descriere | |
|---|---|
| Tip | pavare semiregulată |
| Configurația feței | V3.4.6.4 |
| Simbol Wythoff | 3 | 6 2 |
| Simbol Schläfli | rr{6,3} sau |
| Diagramă Coxeter |      |
| Grup de simetrie | p6m, [6,3], (*632) |
| Grup de rotație | p6, [6,3]+, (632) |
| Poliedru dual | pavare rombitrihexagonală |
| Proprietăți | tranzitivă pe fețe |
În geometrie pavarea trihexagonală romboidală este o duală a pavărilor semiregulate cunoscute sub numele de pavări rombitrihexagonale. Laturile pavări pot fi formate prin suprapunerea intersecțiilor pavării triunghiulare și ale celei hexagonale regulate. Fiecare față romboidală a acestei pavări are unghiurile de 120°, 90°, 60° și 90°. Este una dintre cele opt pavări ale planului în care fiecare latură se află pe o dreaptă de simetrie a pavărilor.[1][2]
Poliedre și pavări înrudite

Este una dintre cele 7 pavări uniforme duale în simetrie hexagonală, inclusiv dualele regulate.
| Simetrie: [6,3], (*632) | [6,3]+, (632) | |||||
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| V63 | V3.122 | V(3.6)2 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 |
Această pavare are variante tranzitive pe fețe, care pot deforma romboizii în trapeze sau patrulatere mai generale. Ignorând culorile feței de mai jos, simetria completă este p6m, iar simetria inferioară este p31m, cu 3 plane de oglindire care se întâlnesc într-un punct, și puncte de rotație cu trei poziții.[3]
| Simetrie | p6m, [6,3], (*632) | p31m, [6,3+], (3*3) | |
|---|---|---|---|
| Formă | 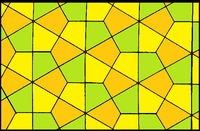 |  | 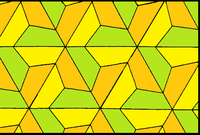 |
| Fețe | Romboizi | Jumătăți de hexagon regulat | Patrulatere |

Această pavare este legată de pavarea trihexagonală prin divizarea triunghiurilor și hexagoanelor în triunghiuri și asamblarea triunghiurilor învecinate în romboedre.
Pavarea trihexagonală romboidală face parte dintr-un set de pavări duale uniforme, corespunzătoare dualelor pavărior rombitrihexagonale.
Variante de simetrie
Această pavare este legată topologic de secvența de pavări cu configurațiile fețelor V3.4.n.4 și continuă cu pavările planului hiperbolic. Aceste figuri tranzitive pe fețe au simetria în notația orbifold (*n32).
| Simetrie *n32 [n,3] | Sferice | Euclid. | Hiperb. compacte | Paracomp. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Config. feței |  V3.4.2.4 |  V3.4.3.4 |  V3.4.4.4 |  V3.4.5.4 |  V3.4.6.4 |  V3.4.7.4 |  V3.4.8.4 |  V3.4.∞.4 |
Alte pavări romboidale
Sunt posibile și alte pavări romboidale.
Simetria față de centru permite ca planul să fie umplut de romboizi cu dimensiuni crescătoare, sau cu o topologie ca a pavării pătrate, V4.4.4.4. Mai jos este un exemplu cu simetrie hexagonală diedrică.
| Simetrie | D6, [6], (*66) | pmg, [∞,(2,∞)+], (22*) | p6m, [6,3], (*632) |
|---|---|---|---|
| Pavare |  |  |  |
| Configurație | V4.4.4.4 | V6.4.3.4 | |
Note
- ^ en Kirby, Matthew; Umble, Ronald (), „Edge tessellations and stamp folding puzzles”, Mathematics Magazine, 84 (4): 283–289, arXiv:0908.3257
 , doi:10.4169/math.mag.84.4.283, MR 2843659
, doi:10.4169/math.mag.84.4.283, MR 2843659 - ^ en Eric W. Weisstein, Dual tessellation la MathWorld. (See comparative overlay of this tiling and its dual)
- ^ Tilings and Patterns
Bibliografie
- en Grünbaum, Branko; Shephard, G. C. (). Tilings and Patterns
 . New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65) - en Williams, Robert, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, Inc., 1979, ISBN: 0-486-23729-X, p/ 40
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 [1] (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings.
- en Eric W. Weisstein, Uniform tessellation la MathWorld.
- en Eric W. Weisstein, Semiregular tessellation la MathWorld.
- en Klitzing, Richard. „2D Euclidean tilings x3o6x - rothat - O8”.
- en Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern N, Dual p. 77-76, pattern 2
- en Dale Seymour, Jill Britton, Introduction to Tessellations, 1989, ISBN: 978-0866514613, pp. 50–56, dual p. 116
Vezi și
Legături externe
 | Portal Matematică |
 Materiale media legate de pavare trihexagonală romboidală la Wikimedia Commons
Materiale media legate de pavare trihexagonală romboidală la Wikimedia Commons

















