Kvaternion

Kvaternion (fra latin quaternio - gruppe med fire) eller Hamilton-tall er et element i en firedimensjonal utvidelse av de reelle tallene på samme måte som et komplekst tall er en todimensjonal utvidelse. Utvidelsen er ikke-kommutativ slik at når to kvaternioner multipliseres sammen, er resultatet avhengig av rekkefølgen til faktorene.

Hver kvaternion Q inngår i en algebra med fire basiselement (1,i,j,k) slik at den kan entydig skrives som

${\displaystyle Q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$

hvor a, b, c og d er reelle tall. Reglene for multiplikasjon av basiselementene ble funnet av William Rowan Hamilton i 1843. Historien sier at dette skjedde da han vandret med sin kone langs Royal Canal i Dublin. Med en kniv risset han de inn i steinen på en nærliggende bro for ikke å glemme dem. Senere ble oppdagelsen hedret med en plakett på samme sted.

Mengden av kvaternioner skrives H eller ${\displaystyle \mathbb {H} }$ etter Hamilton. Da multiplikasjon er avhengig av rekkefølgen, danner den ikke en vanlig tallkropp som de reelle eller komplekse tallene gjør, men en divisjonsring der hvert element Q har en multiplikativ invers Q ^-1. Derfor kan man både både addere, subtrahere, multiplisere og dividere to kvaternioner Q og P med hverandre. Men på samme måte som multiplikasjon, er ikke divisjon lenger entydig da QP ^-1 i allminnelighet er forskjellig fra P ^-1Q.

Ligningen x² + 1 = 0 har ingen løsninger i mengden av reelle tall. Men utvides denne til å inkludere komplekse tall, har den to løsninger i og -i der i = √-1  er den imaginære enheten. I mengden av kvaternioner har den samme ligningen uendelig mange løsninger.

I tillegg til ren matematisk interesse, benyttes kvaternioner også innen teoretisk fysikk hvor de gir en spesiell, kompakt metode til å beskrive rotasjoner i det tredimensjonale rommet. Dette har igjen anvendelser innen datagrafikk, robotikk og beregning av satellittbaner.

Kvaternioner er det enkleste eksempel på hyperkomplekse tall. De kan utvides til en algebra med åtte basiselement som utgjør mengden av oktonioner. Men i motsetning til kvaternionene, er denne divisjonsalgebraen ikke lenger assosiativ slik at i et produkt av tre eller flere oktonioner må rekkefølgen av de binære multiplikasjonene angis.

Basiselement

Et komplekst tall kan skrives som z = a + bi  hvor a og b er reelle tall og er den imaginære enheten. Mengden av slike tall utgjør et todimensjonalt vektorrom med basiselement (1,i) hvor hver vektor har komponentene (a, b). Det samme vektorrommet utgjør også en algebra da produktet av to slike komplekse tall tilhører samme mengde fordi 1i = i  og i² = - 1. Den inverse av hvert komplekst tall kan også entydig finnes.^[1]

Man kan prøve å utvide dette vektorrommet med en ekstra dimensjon ved å innføre en nye, imaginær enhet j som også tilfredsstiller j² = -1. Hvert tall i denne mengden vil da kunne skrives som a + bi  + cj . Ved multiplikasjon av to slike tall, vil da produktet i j oppstå. Skal disse tallene utgjøre en algebra, må dette produktet kunne uttrykkes ved de tre basiselementene (1,i,j ). For å finne ut av egenskapene til dette nye produktet, kan man kvadrere det. Det gir i j i j. Hvis nå i og j kommuterer med hverandre, er dette lik med i²j² = 1. Det betyr at i j = ±1 slik at man må ha i = j eller i = -j. I begge tilfeller er den tredimensjonale utvidelsen i virkeligheten redusert til den opprinnelige i to dimensjoner.

I det motsatte tilfellet hvor de to basiselementene antikommuterer, kalte Hamilton dem for «tripletter». Skriver man dem med fete typer slik at ${\displaystyle \mathbf {i} \mathbf {j} =-\mathbf {j} \mathbf {i} }$, vil dermed ${\displaystyle \mathbf {i} \mathbf {j} \mathbf {i} \mathbf {j} =-\mathbf {i} ^{2}\mathbf {j} ^{2}=-1}$ . Produktet ${\displaystyle \mathbf {i} \mathbf {j} }$ er derfor en imaginær størrelse som Hamilton ikke kunne uttrykke som et element i det tredimensjonale vektorrommet. Han måtte derfor til slutt innføre et fjerde basiselement ${\displaystyle \mathbf {k} =\mathbf {i} \mathbf {j} }$ med ${\displaystyle \mathbf {k} ^{2}=-1}$. På den måten får vektorrommet fire dimensjoner, og alle element har formen ${\displaystyle a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$. Mengden av slike element ga Hamilton navnet kvaternioner.^[2]

Presis definisjon

Multiplikasjon av basiselement

×	1	i	j	k
1	1	i	j	k
i	i	−1	k	−j
j	j	−k	−1	i
k	k	j	−i	−1

Egenskapene til kvaternionene følger direkte fra egenskapene til basiselementene ${\displaystyle (1,\mathbf {i} ,\mathbf {j} ,\mathbf {k} )}$. Disse er entydig gitt ved definisjonene

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i} \mathbf {j} \mathbf {k} =-1}$

som Hamilton opprinnelig kom frem til.^[2] For eksempel, ved å multiplisere ${\displaystyle \mathbf {i} \mathbf {j} \mathbf {k} }$ med ${\displaystyle \mathbf {k} }$ fra høyre, får man ${\displaystyle \mathbf {i} \mathbf {j} =\mathbf {k} }$. Likedan gir en multiplikasjon med ${\displaystyle \mathbf {i} }$ fra venstre at ${\displaystyle \mathbf {j} \mathbf {k} =\mathbf {i} }$. Hvis dette resultatet så multipliseres med ${\displaystyle \mathbf {j} }$ fra venstre, finner man at ${\displaystyle \mathbf {j} \mathbf {i} =-\mathbf {k} }$ slik at disse to basiselementene antikommuterer med hverandre. Slik kan man fortsette og vise at de tre basiselementene ${\displaystyle \mathbf {i} ,\mathbf {j} }$ og ${\displaystyle \mathbf {k} }$ antikommuterer på samme måte. Men fremdeles gjelder ${\displaystyle 1\mathbf {i} =\mathbf {i} 1=\mathbf {i} }$ og tilsvarende for de to andre basiselementene.

Disse detaljerte egenskapene kan sammenfattes som

${\displaystyle {\begin{aligned}\mathbf {i} \mathbf {j} =\mathbf {k} &=-\mathbf {j} \mathbf {i} \\\mathbf {j} \mathbf {k} =\mathbf {i} &=-\mathbf {k} \mathbf {j} \\\mathbf {k} \mathbf {i} =\mathbf {j} &=-\mathbf {i} \mathbf {k} \end{aligned}}}$

Multiplikasjon av to vilkårlige kvaternioner kan nå utføres på en veldefinert måte.

Aritmetiske egenskaper

Da en kvaternion ${\displaystyle Q=q_{0}+q_{1}\mathbf {i} +q_{2}\mathbf {j} +q_{3}\mathbf {k} }$ er et element i et vektorrom, vil den kunne adderes til en annen kvaternion P med resultatet

${\displaystyle Q+P=(q_{0}+p_{0})+(q_{1}+p_{1})\mathbf {i} +(q_{2}+p_{2})\mathbf {j} +(q_{3}+p_{3})\mathbf {k} }$

Herav følger også hvordan differansen mellom to kvaternioner kan finnes. Hvis alle komponentene i resultatet er null, snakker man om en «nullkvaternion» eller ganske enkelt 0.

Fra regnereglene for produkt av basiselement kan multiplikasjon av de to kvaternioner utføres. Som et et konkret eksempel kan man betrakte ${\displaystyle Q=3\mathbf {i} -2\mathbf {j} +\mathbf {k} }$ og ${\displaystyle P=1-3\mathbf {k} }$. Da blir

${\displaystyle {\begin{aligned}QP&=(3\mathbf {i} -2\mathbf {j} +\mathbf {k} )(1-3\mathbf {k} )=3\mathbf {i} -2\mathbf {j} +\mathbf {k} -9\mathbf {ik} +6\mathbf {jk} -3\mathbf {k} \mathbf {k} \\&=3\mathbf {i} -2\mathbf {j} +\mathbf {k} +9\mathbf {j} +6\mathbf {i} +3=3+9\mathbf {i} +7\mathbf {j} +\mathbf {k} \end{aligned}}}$

I det generelle tilfellet gir det kvaternionske produktet

${\displaystyle {\begin{aligned}QP&=(q_{0}p_{0}-q_{1}p_{1}-q_{2}p_{2}-q_{3}p_{3})\\&+(q_{0}p_{1}+q_{1}p_{0}+q_{2}p_{3}-q_{3}p_{2})\,\mathbf {i} \\&+(q_{0}p_{2}-q_{1}p_{3}+q_{2}p_{0}+q_{3}p_{1})\,\mathbf {j} \\&+(q_{0}p_{3}+q_{1}p_{2}-q_{2}p_{1}+q_{3}p_{0})\,\mathbf {k} \end{aligned}}}$

For hver kvaternion ${\displaystyle Q}$ må det også eksistere en invers kvaternion ${\displaystyle Q^{-1}}$ med den egenskapen at ${\displaystyle QQ^{-1}=Q^{-1}Q=1}$ under disse multiplikasjonsreglene.^[1]

Skalar-vektor oppsplitting

Resultatet av slik multiplikasjon kan gjøres mer opplysende ved å splitte en generell kvaternion ${\displaystyle Q}$ med komponentene ${\displaystyle (q_{0},q_{1},q_{2},q_{3})}$ i en skalar del ${\displaystyle q_{0}}$ og en vektoriell del ${\displaystyle \mathbf {q} =q_{1}\mathbf {i} +q_{2}\mathbf {j} +q_{3}\mathbf {k} }$. Den kan da skrives som ${\displaystyle Q=(q_{0},\mathbf {q} )}$. Er den skalare delen lik med null, sies kvaternionen å være vektoriell eller imaginær. Derimot hvis den vektorielle delen er null, er kvaternionen skalar eller reell. For eksempel vil ligningen x² + 1 = 0 ha uendelig mange løsninger som er vektorielle kvaternioner ${\displaystyle X=(0,\mathbf {x} )}$ med x ⋅ x = 1. De ligger på kuleflaten x₁² + x₂² + x₃² = 1  i et tredimensjonalt rom.

Med denne notasjonen kan nå summen av to kvaternioner skrives som ${\displaystyle Q+P=(q_{0}+p_{0},\mathbf {q} +\mathbf {p} )}$, mens deres produkt er gitt som

${\displaystyle QP=(q_{0}p_{0}-\mathbf {q} \cdot \mathbf {p} ,q_{0}\mathbf {p} +p_{0}\mathbf {q} +\mathbf {q} \times \mathbf {p} )}$

Her er nå ${\displaystyle \mathbf {q} \cdot \mathbf {p} =q_{1}p_{1}+q_{2}p_{2}+q_{3}p_{3}}$ det vanlige indreproduktet, mens

${\displaystyle \mathbf {q} \times \mathbf {p} =(q_{2}p_{3}-q_{3}p_{2})\mathbf {i} +(q_{3}p_{1}-q_{1}p_{3})\mathbf {j} +(q_{1}p_{2}-q_{2}p_{1})\mathbf {k} }$

er det tilsvarende kryssproduktet av de to tredimensjonale vektorene. Det følger fra de elementære kryssproduktene

${\displaystyle {\begin{aligned}\mathbf {i} \times \mathbf {j} =\mathbf {k} &=-\mathbf {j} \times \mathbf {i} \\\mathbf {j} \times \mathbf {k} =\mathbf {i} &=-\mathbf {k} \times \mathbf {j} \\\mathbf {k} \times \mathbf {i} =\mathbf {j} &=-\mathbf {i} \times \mathbf {k} \end{aligned}}}$

hvor de diagonale produktene ${\displaystyle \mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =0}$. Det generelle produktet av to vektorielle kvaternioner har en skalar del som er gitt ved indreproduktet av de tilsvarende vektorene og en vektordel som er gitt ved deres kryssproduktet. Mye av denne grunn blir derfor indreproduktet omtalt som et skalert produkt, mens kryssproduktet kalles et vektorprodukt.

Disse likhetstrekkene med vanlig vektoranalyse er ikke overraskene da kryssproduktet som der er av sentral betydning, oppsto i stor grad fra det kvaternionske produktet. Av samme grunn benyttes fremdeles notasjonen ${\displaystyle \mathbf {i} ,\mathbf {j} }$ og ${\displaystyle \mathbf {k} }$ som Hamilton innførte, for de kartesiske basisvektorene i et tredimensjonalt vektorrom.^[3]

Konjugasjon og norm

Størrelsen til et komplekst tall z = a + bi  er gitt ved dets norm N(z) = a² + b². Kvadratroten av denne normen angir lengden |z | til vektoren som fremstiller tallet i det komplekse planet. Normen kan finnes fra det komplekskonjugerte tallet z * = a - bi  ved at N(z) = z z * = z *z = |z |². Normen til et produkt av to komplekse tall z₁  og z₂  vil da oppfylle N(z₁z₂) = N(z₁)N(z₂). Uttrykkes dette resultatet ved komponentene til de to tallene, oppfyller de en «to-kvadrats identitet» som kan føres tilbake til Diofantos.^[4]

På samme måte defineres konjugasjon av en kvaternion ${\displaystyle Q=(q_{0},\mathbf {q} )}$ som

${\displaystyle Q^{*}=(q_{0},-\mathbf {q} )=q_{0}-q_{1}\mathbf {i} -q_{2}\mathbf {j} -q_{3}\mathbf {k} }$

og følger formelt fra ${\displaystyle \mathbf {i} ^{*}=-\mathbf {i} ,\;\mathbf {j} ^{*}=-\mathbf {j} ,\;\mathbf {k} ^{*}=-\mathbf {k} .}$ Ved direkte multiplikasjon kan nå normen finnes fra definisjonen

${\displaystyle N(Q)=QQ^{*}=Q^{*}Q=q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}}$

slik at den er alltid positiv. Den inverse til kvaternionen ${\displaystyle Q}$ er derfor

${\displaystyle Q^{-1}={Q^{*} \over N(Q)}}$

og oppfyller ${\displaystyle QQ^{-1}=Q^{-1}Q=1}$. Divisjon av to generelle kvaternioner ${\displaystyle Q}$ og ${\displaystyle P}$ kan nå gjennomføres, men vil i allminnelighet kunne gi forskjellige resultet avhengig av om man beregner ${\displaystyle PQ^{-1}}$ eller ${\displaystyle Q^{-1}P}$. Definerer man en «enhetskvaternion» ved at dens norm ${\displaystyle N(Q)=1=|Q|^{2}}$, vil den ha en invers som ganske enkelt er ${\displaystyle Q^{-1}=Q^{*}}$.

En konjugasjon av et produkt av to kvaternioner er gitt ved produktet av deres to konjugerte i omvendt rekkefølge, ${\displaystyle (QP)^{*}=P^{*}Q^{*}}$. Det kan man se nødvendigheten av allerede på enkleste nivå. For eksempel, ${\displaystyle (\mathbf {ij} )^{*}=\mathbf {k} ^{*}=-\mathbf {k} =\mathbf {j} ^{*}\mathbf {i} ^{*}.}$ Det betyr at

${\displaystyle N(QP)=QP(QP)^{*}=QPP^{*}Q^{*}=N(Q)N(P)}$

da multiplikasjon er assosiativ. Da hver norm er en sum av fire kvadrat, kalles denne egenskapen «Eulers fire-kvadrats identitet» og er

${\displaystyle {\begin{aligned}&(q_{1}^{2}+q_{2}^{2}+q_{3}^{2}+q_{4}^{2})(p_{1}^{2}+p_{2}^{2}+p_{3}^{2}+p_{4}^{2})\\&=(q_{1}p_{1}-q_{2}p_{2}-q_{3}p_{3}-q_{4}p_{4})^{2}+(q_{1}p_{2}+q_{2}p_{1}+q_{3}p_{4}-q_{4}p_{3})^{2}\\&+(q_{1}p_{3}-q_{2}p_{4}+q_{3}p_{1}+q_{4}p_{2})^{2}+(q_{1}p_{4}+q_{2}p_{3}-q_{3}p_{2}+q_{4}p_{1})^{2}\end{aligned}}}$

Likheten kan føres tilbake til Leonhard Euler som oppdaget den omtrent hundre år før Hamilton konstruerte kvaternionene.^[4]

Rotasjoner

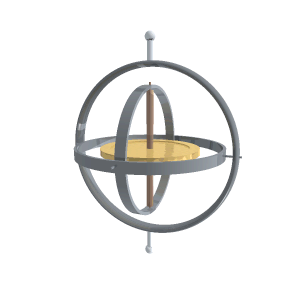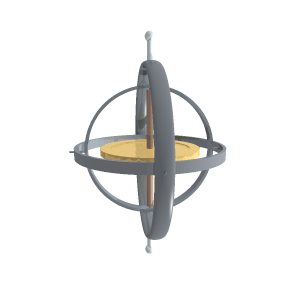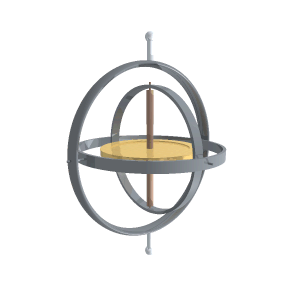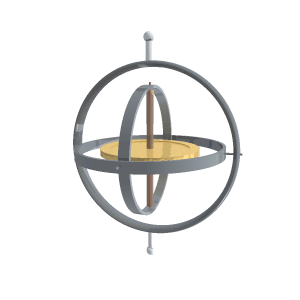
Et komplekst tall z = x + i y kan fremstilles som en vektor i et todimensjonalt plan med kartesiske koordinater (x,y ). Hvis dette tallet multipliseres med et annet komplekst tall e^iθ som har norm |z |² = 1, vil vektoren transformeres på en bestemt måte. Fra Eulers formel har man e^iθ = cosθ + i sinθ slik at den nye vektoren z'  = x'  + i y'  får koordinater x'  = x cosθ - y sinθ  og y'  = x sinθ + y cosθ. Dette representerer en rotasjon av vektoren om en akse som står vinkelrett på planet da dens lengde forblir uforandret.

På en lignende måte kan kvaternioner benyttes til å beskrive rotasjoner i det tredimensjonale rommet. Da de tre basiselementene alle tilfredsstiller ${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1}$ på samme måte som den imaginære enheten i  i to dimensjoner, vil de kunne benyttes til å generere rotasjoner om x-, y- og z-aksen. Disse spesielle transformasjonene er gitt ved de tilsvarende enhetskvarternionene.^[5] For eksempel vil en rotasjon om z-aksen være gitt som

${\displaystyle U=\cos {\theta \over 2}+\mathbf {k} \sin {\theta \over 2}=e^{\mathbf {k} \theta /2}}$

Den inverse transformasjonen ${\displaystyle U^{-1}=U^{*}}$ tilsvarer nå en rotasjonsvinkel -θ som forventet. Ved direkte utregning finner man herav

${\displaystyle U\mathbf {i} U^{-1}=\cos \theta \,\mathbf {i} +\sin \theta \,\mathbf {j} }$

${\displaystyle U\mathbf {j} U^{-1}=\cos \theta \,\mathbf {j} -\sin \theta \,\mathbf {i} }$

mens basiselementet ${\displaystyle \mathbf {k} }$ forblir uforandret. Hvis man representerer en generell vektor i rommet ved den sektorielle kvaternionen ${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} ,}$ vil den dermed transformeres til

${\displaystyle \mathbf {r'} =U\mathbf {r} U^{-1}=(x\cos \theta -y\sin \theta )\mathbf {i} +(x\sin \theta +y\cos \theta )\mathbf {j} +z\mathbf {k} }$

under en rotasjon om z-aksen. Den viser den forventede forandringen av koordinatene normalt til rotasjonsaksen. Allerede året etter at Hamilton hadde etablert kvaternionene, viste Arthur Cayley at de kunne forbindes med slike romlige rotasjoner.^[6]

Generell rotasjon

Denne formalismen kan direkte utvides til å beskrive en rotasjon om en vilkårlig akse ${\displaystyle \mathbf {n} =n_{x}\mathbf {i} +n_{y}\mathbf {j} +n_{z}\mathbf {k} .}$ Velges den med norm ${\displaystyle \mathbf {n} \cdot \mathbf {n} =1,}$ er transformasjonen gitt ved enhetskvaternionen

${\displaystyle U=e^{\mathbf {n} \theta /2}=\cos {\theta \over 2}+\mathbf {n} \sin {\theta \over 2}}$

der θ er rotasjonsvinkelen om denne aksen. Da produktet av to slike kvaternioner ${\displaystyle e^{\mathbf {a} \alpha /2}}$ og ${\displaystyle e^{\mathbf {b} \beta /2}\;}$vil gi en ny enhetskvaternion, danner rotasjonene en kontinuerlig Lie-gruppe som er SU(2).^[7] Eksplisitt kan man se det ved direkte utregning av kvaternionproduktet

${\displaystyle e^{\mathbf {a} \alpha /2}e^{\mathbf {b} \beta /2}=e^{\mathbf {c} \gamma /2}}$

som tilsvarer en rotasjon med en vinkel γ gitt ved

${\displaystyle \cos {\gamma \over 2}=\cos {\alpha \over 2}\cos {\beta \over 2}-\mathbf {a} \cdot \mathbf {b} \sin {\alpha \over 2}\sin {\beta \over 2}}$

Dette uttrykket representerer cosinussetningen i sfærisk geometri.^[5] Den tilsvarende rotasjonsaksen c finnes fra

${\displaystyle \mathbf {c} \sin {\gamma \over 2}=\mathbf {a} \sin {\alpha \over 2}\cos {\beta \over 2}+\mathbf {b} \sin {\beta \over 2}\cos {\alpha \over 2}+\mathbf {a} \times \mathbf {b} \sin {\alpha \over 2}\sin {\beta \over 2}}$

Grunnen til at de halve rotasjonsvinklene opptrer i denne formalismen, er forbundet med at kvaternionene kan avbildes på de todimensjonale matrisene som Pauli fant for kvantemekaniske partikler med spinn S = 1/2.^[8]

Rodrigues' rotasjonsformel

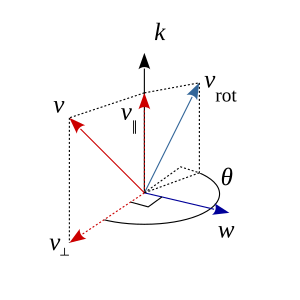
En generell rotasjon kan angis ved tre rotasjonsvinkler eller en vinkel θ om en akse n med lengde 1. En vektor r transformeres dermed til en ny vektor

${\displaystyle \mathbf {r} \rightarrow \mathbf {r'} =e^{\mathbf {n} \theta /2}\mathbf {r} e^{-\mathbf {n} \theta /2}}$

Her er nå både ${\displaystyle \mathbf {n} }$ og ${\displaystyle \mathbf {r} }$ vektorielle kvaternioner slik at for eksempel ${\displaystyle \mathbf {n} \mathbf {r} =-\mathbf {n} \cdot \mathbf {r} +\mathbf {n} \times \mathbf {r} }$. Mens skalarproduktet er et reelt tall, er kryssproduktet en ny, vektoriell kvaternion. På den måten blir den transformerte vektoren

${\displaystyle \mathbf {r'} =\mathbf {r} \cos \theta +\mathbf {n} \times \mathbf {r} \sin \theta +\mathbf {n} (\mathbf {n} \cdot \mathbf {r} )(1-\cos \theta )}$

Dette resultatet kalles Rodrigues' rotasjonsformel etter Olinde Rodrigues som fant den på midten av 1800-tallet.^[9]

Da r er en vektor et et 3-dimensjonalt rom, er det også mulig å skrive den transformerte vektoren som en 3 × 3 rotasjonsmatrise som virker på den.^[10] Ved å definere den antisymmetriske matrisen

${\displaystyle N=\left[{\begin{array}{ccc}0&-n_{z}&n_{y}\\n_{z}&0&-n_{x}\\-n_{y}&n_{x}&0\end{array}}\right]}$

kan man skrive kryssproduktet n × r = N r. Derfor er også N²r = n ×(n × r) = n(n ⋅ r) - r.

Matrisen har den viktige egenskapen at N³ = - N  som følger fra n_x² + n_y² + n_z² = 1. Den roterte vektoren er nå r'  = M r  hvor rotasjonsmatrisen kan skrives på den kompakte formen

${\displaystyle {\begin{aligned}M=e^{\theta N}&=1+\theta N+\theta ^{2}{N^{2} \over 2!}+\theta ^{3}{N^{3} \over 3!}+\theta ^{4}{N^{4} \over 4!}+\cdots \\&=1+\sin \theta N+(1-\cos \theta )N^{2}\end{aligned}}}$

når man benytter Taylor-utviklingen for eksponentialfunksjonen av en matrise. Disse 3-dimensjonale rotasjonsmatrisene representerer Lie-gruppen SO(3).^[7]

Andre representasjoner

Så tidlig som i 1835 hadde Hamilton vist at et komplekse tallet z = a + i b kan representeres ved et par av reelle tall (a,b). Den konjugert partner er da z* = (a,-b) slik at den imaginære enheten kan skrives som i = (0,1). Produktet av to komplekse tall z = (a,b) og w = (c,d) er definert som

${\displaystyle (a,b)(c,d)=(ac-bd,ad+bc)}$

som oppfyller i² = (0,1)(0,1) = (-1,0) = -1. Normen til z er derfor N(z) = z*z = (a² + b², 0). Alle andre egenskaper til disse tallene følger herav uten å benytte eksplisitt at den imaginære enheten har et kvadrat som er negativ.^[1]

I samme arbeid som Cayley viste hvordan kvarternionene kunne forbindes med rotasjoner i et tredimensjonalt rom, viste han også hvordan de kunne representeres ved et lignende par med tall, men i dette tilfellet komplekse tall.^[6] Denne muligheten kan man se ved å omskrive det generelle uttrykket for en kvaternion,

${\displaystyle Q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =(a+b\mathbf {i} )+(c+d\mathbf {i} )\mathbf {j} }$

Det har formen av et komplekst tall (z, w) = z + w j med j² = -1, men med komplekse element z = a + b i  og w = c + d i hvor i² = -1 og i j = k. De tre imaginære enhetene kan nå unngås ved å definere en kvaternion som Q = (z,w) hvor det komplekse tallparet består av z = a + i b og w = c + i d med i² = -1.

Produktet av to kvaternioner er definert som

${\displaystyle Q_{1}Q_{2}=(z_{1}z_{2}-w_{1}w_{2}^{*},z_{1}w_{2}+w_{1}z_{2}^{*})}$

Hvis nå den konjugerte kvaternionen defineres som (z,w)* = (z*, - w), blir dens norm

${\displaystyle Q^{*}Q=(z^{*},-w)(z,w)=(z^{*}z+w^{*}w,0)}$

som er et reelt tall. I ettertid er denne representasjonen av kvaternioner blitt kalt for «Cayley-Dickson-konstruksjonen». Det er mulig å konstruere oktonioner fra kvaternioner med samme metode.^[11]

Matriserepresentasjoner

Etter at Cayley innførte regnereglene for matriser i 1858, ble det klart at Hamiltons representasjon (a,b) for det komplekse tallet z = a + i b var ekvivalent med bruk av 2×2 matriser.^[12] Det gjøres ved å skrive

${\displaystyle z={\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&\;\;0\end{pmatrix}}}$

hvor det reelle tallet 1 = (1,0) er erstattet med identitetsmatrisen i to dimensjoner og den imaginære enheten i = √-1  med

${\displaystyle i={\begin{pmatrix}0&-1\\1&\;\;0\end{pmatrix}}.}$

Regelen for produkt av komplekse tall er nå en konsekvens av regelen for vanlig multiplikasjon av matriser,

${\displaystyle zw={\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}{\begin{pmatrix}c&-d\\d&\;\;c\end{pmatrix}}={\begin{pmatrix}ac-bd&-ad-bc\\ad+bc&\;\;ac-bd\end{pmatrix}}}$

Kompleks konjugasjon følger fra å ta den transponerte av matrisen. Alle egenskaper til de komplekse tallene følger nå fra denne matriserepresentasjonen.^[11]

Ved å la elementene i slike 2×2 matriser bli komplekse, kan en kvaternion Q = (z,w) representeres på samme måte som

${\displaystyle Q={\begin{pmatrix}z&-w\\w^{*}&\;\;z^{*}\end{pmatrix}}}$

Resultatet for produktet av to kvaternioner ${\displaystyle Q_{1}}$ og ${\displaystyle Q_{2}}$ følger nå fra vanlig matrisemultiplikasjon. Den konjugerte ${\displaystyle Q^{\dagger }}$ av kvaternionen beregnes i denne representasjonen ved en kombinert transponering av matrisen fulgt av vanlig komplekskonjugasjon, det vil si hermitsk konjugasjon. Det gir

${\displaystyle Q^{\dagger }={\begin{pmatrix}\;\;z^{*}&w\\-w^{*}&z\end{pmatrix}}}$

slik at ${\displaystyle Q^{\dagger }Q=QQ^{\dagger }=\det Q=z^{*}z+w^{*}w}$. Den tilsvarende representasjonen av basiselementene finnes fra oppsplittingen z = a + i b og w = c + i d. Man har da

${\displaystyle Q={\begin{pmatrix}a+ib&-c-id\\c-id&\;\;a-ib\end{pmatrix}}=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$

med

${\displaystyle 1={\begin{pmatrix}1&0\\0&1\end{pmatrix}},\;\;\mathbf {i} ={\begin{pmatrix}i&\;\;0\\0&-i\end{pmatrix}},\;\;\mathbf {j} ={\begin{pmatrix}0&-1\\1&\;\;0\end{pmatrix}},\;\;\mathbf {k} ={\begin{pmatrix}\;\;0&-i\\-i&\;\;0\end{pmatrix}}.}$

Istedenfor denne representasjonen med 2×2 komplekse matriser, kan man også konstruere representasjoner av kvaternionene med 4×4 matriser reelle matriser. Men for praktiske beregninger er disse mindre anvendelige.^[5]

Pauli-matriser

I den todimensjonale representasjonen skifter basiselementene fortegn under hermitisk konjugasjon. De tilsvarende matriser som er invariante under denne operasjonen, er de tre Pauli-matrisene som benyttes i kvantemekanikken til rotasjoner av partikler med spinn s = 1/2. I den sammenhengen er de representert ved matrisene^[8]

${\displaystyle \sigma _{1}={\begin{pmatrix}0&\;\;1\\1&\;\;0\end{pmatrix}},\;\;\sigma _{2}={\begin{pmatrix}0&-i\\i&\;\;0\end{pmatrix}},\;\;\sigma _{3}={\begin{pmatrix}1&\;\;0\\0&-1\end{pmatrix}}}$

De skiller seg med i = √-1  fra de kvaternionske basiselementene ved sammenhengene i = i σ₃, j = -i σ₂ og k = -i σ₁. Men matriserepresentasjonen av kvaternionene er ikke entydig. Den kan alternativt like godt defineres ved sammenhengene i = -i σ₁, j = -i σ₂ og k = -i σ₃ slik at

${\displaystyle Q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} ={\begin{pmatrix}a-id&-c-ib\\c-ib&\;\;a+id\end{pmatrix}}}$

Forskjellige produkt mellom basiselementene kan da uttrykkes ved Pauli-matrisene som

${\displaystyle \sigma _{a}\sigma _{b}=\delta _{ab}+i\varepsilon _{abc}\sigma _{c}}$

hvor δ_ab  er Kronecker-deltaet og ε_abc  er Levi-Civita-symbolet i tre dimensjoner. Man benytter Einsteins summekonvensjon for de to like indeksene i det siste leddet. Alternativt kan man skrive denne fundamentale relasjonen på en mer gjenkjennelig form ved å innføre vektoren σ = (σ₁, σ₂, σ₃). For to vanlige vektorer a og b er da

${\displaystyle ({\boldsymbol {\sigma }}\cdot \mathbf {a} )({\boldsymbol {\sigma }}\cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {b} +i{\boldsymbol {\sigma }}\cdot (\mathbf {a} \times \mathbf {b} )}$

Dette uttrykket fra kvantemekanikken inneholder nå alle egenskapene til kvaternionene.

Se også

• Oktonioner

Referanser

Litteratur

• J.H. Conway and D.A. Smith, On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, CRC Press, Boca Raton (2003). ISBN 978-1-56881-134-5.

Eksterne lenker

• Institutt for Biovitenskap, UiO, Hyperkomplekse tall og kvaternioner
• E.W. Weisstein, Quaternion, from MathWorld