Małe twierdzenie Fermata

Małe twierdzenie Fermata (MTF) – twierdzenie teorii liczb sformułowane (bez dowodu) przez francuskiego matematyka Pierre’a de Fermata. Twierdzenie jest podstawą dla testu pierwszości Fermata. Poniżej każdego sformułowania twierdzenia znajduje się zapis w arytmetyce modularnej.

Małe twierdzenie Fermata:

jeżeli ${\displaystyle p}$ jest liczbą pierwszą, to dla dowolnej liczby całkowitej ${\displaystyle a,}$ liczba ${\displaystyle a^{p}-a}$ jest podzielna przez ${\displaystyle p.}$

${\displaystyle a^{p}-a\equiv 0{\pmod {p}},}$

lub inaczej^[1]:

jeśli ${\displaystyle p}$ jest liczbą pierwszą, a ${\displaystyle a}$ jest taką liczbą całkowitą, że liczby ${\displaystyle a}$ i ${\displaystyle p}$ są względnie pierwsze, to ${\displaystyle a^{p-1}-1}$ dzieli się przez ${\displaystyle p.}$ Innymi słowy,

${\displaystyle a^{p-1}-1\equiv 0{\pmod {p}},}$

albo

${\displaystyle a^{p-1}\equiv 1{\pmod {p}}.}$

Dowody

Dowód z twierdzeniem Eulera

Jeżeli ${\displaystyle p}$ jest taką liczbą pierwszą, która nie dzieli ${\displaystyle a,}$ to ${\displaystyle p}$ jest względnie pierwsze z ${\displaystyle a,}$ a więc w myśl twierdzenia Eulera o liczbach względnie pierwszych teza twierdzenia jest prawdziwa.

Dowód kombinatoryczny

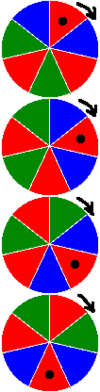
Bez straty ogólności można założyć, że ${\displaystyle a}$ jest liczbą naturalną. Rozpatrzmy wszystkie możliwe kolorowania koła podzielonego na p części za pomocą a kolorów. Kolorowania, które możemy na siebie nałożyć po obróceniu, liczymy jako dwa różne. Wszystkich kolorowań jest ${\displaystyle a^{p}.}$

Wszystkie kolorowania, w których wykorzystaliśmy co najmniej dwa kolory możemy obracać tak, że otrzymamy zestawy po p parami różnych kolorowań, które są swoimi obrotami (przykładowe cztery z pewnego zestawu dla p=7, a=3 są przedstawione na rysunku). Jeżeli w pewnym zestawie utworzonym w ten sposób wystąpiłyby takie same kolorowania, to oznaczałoby to, że kąt pełny jest wielokrotnością pewnego kąta ${\displaystyle {\tfrac {2\pi n}{p}},}$ o który trzeba obrócić jedno z tych kolorowań, aby otrzymać drugie. W przypadku, gdy wykorzystaliśmy jeden kolor, nie jest to możliwe. Zatem:

liczba wszystkich kolorowań jest iloczynem ${\displaystyle p}$ i liczby zestawów po p kolorowań + liczba kolorowań jednokolorowych

${\displaystyle a^{p}=pn+a,}$

gdzie n jest pewną liczbą naturalną.

Kolorów jest a, więc kolorowań jednokolorowych też jest a. Wynika stąd, że ${\displaystyle p}$ dzieli liczbę ${\displaystyle a^{p}-a.}$

Dowód wykorzystujący metody teorii grup

Zbiór ${\displaystyle \mathbb {Z} _{p}^{*}=\{1,\dots ,p-1\}}$ jest grupą z działaniem mnożenia modulo p, nazywaną multiplikatywną grupą klas reszt modulo p. Grupa ta jest rzędu ${\displaystyle p-1}$ (ma ${\displaystyle p-1}$ elementów). Niech ${\displaystyle a}$ będzie dowolnym elementem tej grupy. Oznaczmy przez ${\displaystyle k}$ rząd tego elementu, tzn. najmniejszą liczbę ${\displaystyle k\in \mathbb {N} }$ spełniającą warunek ${\displaystyle a^{k}=1.}$ Innymi słowy

${\displaystyle a^{k}\equiv 1{\pmod {p}}.}$

Z twierdzenia Lagrange’a wynika, że rząd elementu ${\displaystyle a}$ dzieli rząd grupy ${\displaystyle \mathbb {Z} _{p}^{*},}$ czyli ${\displaystyle k|p-1.}$ A zatem istnieje pewna liczba naturalna ${\displaystyle m}$ spełniająca warunek

${\displaystyle p-1=km.}$

Wówczas

${\displaystyle a^{p-1}\equiv a^{km}\equiv (a^{k})^{m}\equiv 1^{m}\equiv 1{\pmod {p}}.}$

Dowód indukcyjny

Załóżmy, że ${\displaystyle a}$ jest liczbą naturalną. Twierdzenie to jest prawdziwe, gdy ${\displaystyle a=1.}$ Zatem załóżmy indukcyjnie, że:

${\displaystyle a^{p}\equiv a{\pmod {p}}}$ dla ${\displaystyle a\geqslant 1.}$

Wówczas:

${\displaystyle (a+1)^{p}=\sum _{k=0}^{p}{p \choose k}a^{k}=a^{p}+a^{0}+\sum _{k=1}^{p-1}{p \choose k}a^{k}.}$

Ponieważ

${\displaystyle {p \choose k}={\frac {p(p-1)(p-2)\dots (p-k+1)}{k!}},}$

więc dla ${\displaystyle 0<k<p}$ żaden z czynników ${\displaystyle k!}$ nie jest równy ${\displaystyle p,}$ dlatego ${\displaystyle p \choose k}$ jest wielokrotnością ${\displaystyle p.}$ Zatem:

${\displaystyle {p \choose k}\equiv 0{\pmod {p}}.}$

Ostatecznie:

${\displaystyle (a+1)^{p}\equiv a^{p}+a^{0}+\sum _{k=1}^{p-1}{p \choose k}a^{k}\equiv a^{p}+a^{0}\equiv a+1.}$

Zatem na mocy indukcji ${\displaystyle a^{p}\equiv a{\pmod {p}},}$ czyli p dzieli ${\displaystyle a^{p}-a.}$

Zobacz też

• liczby pseudopierwsze

Przypisy

Bibliografia

• Wacław Sierpiński: Arytmetyka teoretyczna. Wyd. 2. Warszawa: Państwowe Wydawnictwo Naukowe, 1959, s. 144–147.

Linki zewnętrzne

• TomaszT. Kazana TomaszT., Małe Twierdzenie Fermata, [w:] pismo „Delta”, deltami.edu.pl, kwiecień 2017, ISSN 0137-3005 [dostęp 2022-07-20]  (pol.).
• Eric W.E.W. Weisstein Eric W.E.W., Fermat’s Little Theorem, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2022-07-02].
• Fermat's little theorem (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].