Odwzorowanie azymutalne równopowierzchniowe

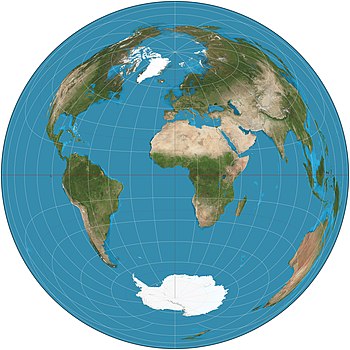
Odwzorowanie azymutalne równopowierzchniowe (azymutalne Lamberta) – odwzorowanie azymutalne, w którym obszary o równej powierzchni na kuli ziemskiej są przedstawiane przez obszary o równej powierzchni na mapie.

Wzory przekształcające to:

${\displaystyle k=\alpha {\sqrt {\frac {2}{1+\sin \phi _{0}\sin \phi +\cos \phi _{0}\cos \phi \cos(\lambda -\lambda _{0})}}}}$

${\displaystyle x=k\cos \phi \sin(\lambda -\lambda _{0})}$

${\displaystyle y=k{\Big (}\cos \phi _{0}\sin \phi -\sin \phi _{0}\cos \phi \cos(\lambda -\lambda _{0}){\Big )}}$

gdzie:

${\displaystyle \lambda }$ – długość geograficzna

${\displaystyle \phi }$ – szerokość geograficzna

${\displaystyle \lambda _{0}}$ – długość punktu centralnego mapy

${\displaystyle \phi _{0}}$ – szerokość punktu centralnego mapy

${\displaystyle \alpha }$ – stała skalowania mapy

Wzory odwrotne:

${\displaystyle \rho ={\frac {\sqrt {x^{2}+y^{2}}}{\alpha }}}$

${\displaystyle z=2\arcsin \left({\frac {\rho }{2}}\right)}$

${\displaystyle \phi =\arcsin \left(\sin \phi _{0}\cos z+{\frac {y\cos \phi _{0}\sin z}{\rho }}\right)}$

${\displaystyle \lambda =\lambda _{0}+\operatorname {arctg} _{2}{\Big (}x\sin z\cos \phi _{0},(\cos z-\sin \phi _{0}\sin \phi )\rho {\Big )}}$