Sfera Riemanna

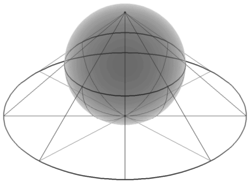
Sfera Riemanna lub płaszczyzna zespolona domknięta – sfera otrzymana z płaszczyzny zespolonej przez dodanie punktu w nieskończoności. Sfera jest geometryczną prezentacją rozszerzonego zbioru liczb zespolonych ${\displaystyle \mathbb {C} \cup \{\infty \},}$ który zawiera wszystkie liczby zespolone oraz obiekt reprezentujący nieskończoność i oznaczany symbolem ${\displaystyle \infty .}$ Nazwa pochodzi od matematyka z XIX wieku Bernharda Riemanna.

Rozszerzony zbiór liczb zespolonych jest przydatny w analizie zespolonej, ponieważ pozwala w pewnych przypadkach na dzielenie przez zero, tzn. wyrażenia takie jak ${\displaystyle 1/0=\infty }$ mają „wartość” w zbiorze ${\displaystyle \mathbb {C} \cup \{\infty \}.}$ Na przykład każda funkcja wymierna na płaszczyźnie zespolonej może być określona jako funkcja ciągła na sferze Riemanna, jeśli biegunom tej funkcji przypiszemy wartość ${\displaystyle \infty .}$ Bardziej ogólnie, każdą funkcję meromorficzną można traktować jako funkcję ciągłą, której przeciwdziedziną jest sfera Riemanna.

W geometrii sfera Riemanna jest przykładem powierzchni Riemanna i jedną z najprostszych rozmaitości zespolonych.

Płaszczyzna zespolona domknięta

Płaszczyznę zespoloną domkniętą ${\displaystyle {\overline {\mathbb {C} }}}$ można uzyskać, uzupełniając płaszczyznę zespoloną punktem oznaczanym przez ${\displaystyle \infty }$^[1]. W tak zdefiniowanym zbiorze określa się topologię, której bazą zbiorów otwartych jest suma zbioru kół otwartych w płaszczyźnie zespolonej i sum dopełnień kół domkniętych w płaszczyźnie zespolonej i zbioru ${\displaystyle \{\infty \}{:}}$

${\displaystyle {\mathfrak {B}}=\bigcup _{a\in \mathbb {C} ,\,r\in \mathbb {R} _{+}}\{z\in \mathbb {C} :|z-a|<r\}\cup \bigcup _{a\in \mathbb {C} ,\,r\in \mathbb {R} _{+}}{\bigg (}\{z\in \mathbb {C} :|z-a|>r\}\cup \{\infty \}{\bigg )}.}$

Zgodnie z tak zwanym twierdzeniem Aleksandrowa tak określona przestrzeń topologiczna jest przestrzenią zwartą (bo płaszczyzna zespolona jest lokalnie zwarta)^[2] Tak określona przestrzeń topologiczna jest homeomorficzna ze sferą w przestrzeni euklidesowej trójwymiarowej ${\displaystyle \mathbb {R} ^{3}=\{(\xi ,\eta ,\zeta ):\xi ,\eta ,\zeta \in \mathbb {R} \}}$ określoną wzorem:

${\displaystyle \{(\xi ,\eta ,\zeta ):\xi ^{2}+\eta ^{2}+\zeta ^{2}-\zeta =0\}.}$

Jest to sfera o środku ${\displaystyle (0,0,{\tfrac {1}{2}})}$ i promieniu ${\displaystyle {\tfrac {1}{2}}.}$ Należą do niej zarówno punkt ${\displaystyle (0,0,0),}$ jak i ${\displaystyle (0,0,1).}$ Płaszczyzna rozpięta na osiach ${\displaystyle \xi }$ i ${\displaystyle \eta }$ jest do tej sfery styczna w punkcie ${\displaystyle (0,0,0).}$ Po utożsamieniu osi ${\displaystyle \xi }$ i ${\displaystyle \eta }$ odpowiednio z osiami ${\displaystyle x}$ i ${\displaystyle y}$ można zastosować rzut stereograficzny płaszczyzny zespolonej domkniętej na tę sferę, który:

• punktowi ${\displaystyle \infty \in {\overline {\mathbb {C} }}}$ przyporządkowuje punkt ${\displaystyle (0,0,1),}$
• każdemu punktowi ${\displaystyle z\neq \infty }$ przyporządkowuje punkt przecięcia powierzchni sfery z prostą łączącą punkty ${\displaystyle z}$ i ${\displaystyle (0,0,1).}$

Rzut ten ustala homeomorfizm między płaszczyzną zespoloną domkniętą a sferą^[3].

Płaszczyzna zespolona domknięta jest pojęciem często używanym w analizie zespolonej.

Przykłady zastosowania

• Funkcja homograficzna ${\displaystyle w={\frac {az+b}{cz+d}},}$ gdzie ${\displaystyle ad-bc\neq 0}$ jest homeomorfizmem przestrzeni ${\displaystyle {\overline {\mathbb {C} }}}$ na siebie. Przekształcenie to jest konforemne we wszystkich punktach ${\displaystyle {\overline {\mathbb {C} }}}$^[4].
• Każda funkcja meromorficzna w ${\displaystyle {\overline {\mathbb {C} }}}$ jest funkcją wymierną^[5].
• Niech ${\displaystyle \gamma }$ będzie krzywą gładką, a ${\displaystyle f}$ funkcją ciągłą na ${\displaystyle \gamma .}$ Wtedy funkcja

${\displaystyle F(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(\zeta )d\zeta }{\zeta -z}}}$

jest funkcją holomorficzną na zbiorze ${\displaystyle {\overline {\mathbb {C} }}\setminus \gamma ,}$ równą zero w ${\displaystyle \infty }$^[6].

Rozszerzony zbiór liczb zespolonych

Rozszerzony zbiór liczb zespolonych zawiera wszystkie liczby zespolone oraz ∞. Zbiór ten można zapisać jako ${\displaystyle \mathbb {C} \cup \{\infty \}}$ i często jest oznaczany przez ozdobienie litery ${\displaystyle \mathbb {C} }$ jakimś symbolem np.:

${\displaystyle {\hat {\mathbb {C} }},\quad {\overline {\mathbb {C} }}\quad {\text{lub}}\quad \mathbb {C} _{\infty }.}$

Rozszerzony zbiór liczb zespolonych jest utożsamiany geometrycznie ze sferą Riemanna.

Operacje arytmetyczne

Dodawanie liczb zespolonych można rozszerzyć przez zdefiniowanie

${\displaystyle z+\infty =\infty ,\quad \infty +\infty =\infty }$

dla dowolnej liczby zespolonej ${\displaystyle z.}$

Mnożenie można rozszerzyć przez zdefiniowanie

${\displaystyle z\cdot \infty =\infty ,\quad \infty \cdot \infty =\infty }$

dla wszystkich liczb zespolonych oprócz zera. Należy jednak zauważyć, że operacje ${\displaystyle \infty -\infty }$ i ${\displaystyle 0\cdot \infty }$ pozostają nieokreślone.

W przeciwieństwie do liczb zespolonych, rozszerzony zbiór liczb zespolonych nie jest ciałem, ponieważ ∞ nie ma liczby odwrotnej. Niemniej jednak zwyczajowo definiuje się w zbiorze ${\displaystyle \mathbb {C} \cup \{\infty \}}$ dzielenie jako

${\displaystyle {\frac {z}{0}}=\infty ,\quad {\frac {z}{\infty }}=0,\quad {\frac {\infty }{0}}=\infty ,\quad {\frac {0}{\infty }}=0}$

dla wszystkich liczb zespolonych ${\displaystyle z}$ oprócz zera.

Funkcje wymierne

Na sferze Riemanna każda funkcja wymierna ${\displaystyle f(z)=g(z)/h(z)}$ może być rozszerzona do funkcji ciągłej. W szczególności, jeśli ${\displaystyle z_{0}}$ jest liczbą zespoloną taką, że mianownik ${\displaystyle h(z_{0})=0}$ natomiast licznik ${\displaystyle g(z_{0})\neq 0}$ to można zdefiniować, że ${\displaystyle f(z_{0})=\infty .}$ Ponadto ${\displaystyle f(\infty )}$ można zdefiniować jako granicę ${\displaystyle f(\infty )=\lim _{z\to \infty }f(z).}$

Przykład: mając daną funkcję

${\displaystyle f(z)={\frac {6z+1}{2z-10}},}$

można zdefiniować ${\displaystyle f(5)=\infty }$ ponieważ mianownik wynosi zero dla ${\displaystyle z=5}$ i ${\displaystyle f(\infty )=3}$ ponieważ ${\displaystyle \lim _{z\to \infty }f(z)=3.}$ Dzięki tym definicjom, funkcja ${\displaystyle f}$ staje się funkcją ciągłą odwzorowującą sferę Riemanna na sferę Riemanna.

Gdy rozpatrujemy sferę Riemanna jako rozmaitość zespoloną okazuje się, że funkcje wymierne są funkcjami holomorficznymi odwzorowującymi ją na siebie.

Rozmaitość zespolona

Sferę Riemanna można uznać za jednowymiarową rozmaitość zespoloną, którą można opisać za pomocą dwóch map o przekształceniach w płaszczyznę zespoloną ${\displaystyle \mathbb {C} .}$ Niech ${\displaystyle \zeta }$ i ${\displaystyle \xi }$ są zespolonymi współrzędnymi na ${\displaystyle \mathbb {C} .}$ Można utożsamiać niezerowe wartości ${\displaystyle \zeta }$ z niezerowymi wartościami ${\displaystyle \xi ,}$ korzystając z przekształceń przejścia

${\displaystyle {\begin{aligned}\zeta &=1/\xi ,\\[8pt]\xi &=1/\zeta .\end{aligned}}}$

Ponieważ przekształcenia przejścia są holomorficzne, definiują one rozmaitość zespoloną nazywaną sferą Riemanna.

Intuicyjnie, przekształcenia przejścia wskazują jak skleić razem dwie płaszczyzny aby utworzyć sferę Riemanna. Płaszczyzny są sklejone w sposób „wewnątrz-na-zewnątrz”, czyli nakładają się na siebie niemalże całkowicie, jedynie środki płaszczyzn (tj. punkty zerowe) są indywidualnym wkładem dopełniającym braki jednej względem drugiej. Innymi słowy (prawie) każdy punkt na sferze Riemanna ma przypisane dwie wartości ${\displaystyle \zeta }$ i ${\displaystyle \xi ,}$ które łączy relacja ${\displaystyle \zeta =1/\xi .}$ Punkt, w którym ${\displaystyle \xi =0,}$ powinien mieć wartość „1/0”; w tym znaczeniu środek płaszczyzny będącej mapą ${\displaystyle \xi }$ pełni rolę „${\displaystyle \infty }$” na mapie ${\displaystyle \zeta }$ i odwrotnie.

Od strony topologicznej uzyskana przestrzeń jest uzwarceniem jednopunktowym płaszczyzny. Jednakże sfera Riemanna to nie tylko sfera topologiczna. Ta sfera ma dobrze zdefiniowaną strukturę zespoloną, tj. dla każdego punktu na sferze istnieje otoczenie które może być utożsamione za pomocą bijekcji holomorficznej z ${\displaystyle \mathbb {C} .}$

Z drugiej strony, twierdzenie o ujednoliceniu (centralny wynik klasyfikacji powierzchni Riemanna) stanowi, że jednospójnymi jednowymiarowymi rozmaitościami zespolonymi są tylko płaszczyzna zespolona, płaszczyzna hiperboliczna i sfera Riemanna. Z tego zbioru jedynie sfera Riemanna jest rozmaitością zamkniętą (zwartą i bez brzegu). Stąd dwuwymiarowa sfera uzyskuje jednoznaczną strukturę zespoloną, przekształcając się w jednowymiarową rozmaitość zespoloną.

Sfera

Sferę Riemanna można przedstawić jako sferę jednostkową ${\displaystyle x^{2}+y^{2}+z^{2}=1}$ w trójwymiarowej przestrzeni rzeczywistej ${\displaystyle \mathbb {R} ^{3}.}$ Aby to osiągnąć należy zastosować rzut stereograficzny sfery jednostkowej bez punktu ${\displaystyle (0,0,1)}$ na płaszczyznę ${\displaystyle z=0,}$ którą utożsamia się z płaszczyzną zespoloną za pomocą ${\displaystyle \zeta =x+iy.}$ Współrzędne kartezjańskie ${\displaystyle (x,y,z)}$ i sferyczne ${\displaystyle (\varphi ,\theta )}$ na sferze (gdzie ${\displaystyle \varphi }$ to odległość zenitalna, a ${\displaystyle \theta }$ to długość azymutalna) opisuje równanie

${\displaystyle \zeta ={\frac {x+iy}{1-z}}=\operatorname {ctg} (\phi /2)\;e^{i\theta }.}$

Podobnie, rzut stereograficzny od ${\displaystyle (0,0,-1)}$ na płaszczyznę ${\displaystyle z=0,}$ utożsamiany z inną kopią płaszczyzny jako ${\displaystyle \xi =x-iy,}$ opisuje równanie

${\displaystyle \xi ={\frac {x-iy}{1+z}}=\operatorname {tg} (\phi /2)\;e^{-i\theta }.}$

Aby pokryć całą sferę jednostkową potrzebne są dwa odwzorowania: pierwsze przekształca całą sferę z wyjątkiem punktu ${\displaystyle (0,0,1)}$ a drugie podobnie z wyjątkiem punktu ${\displaystyle (0,0,-1).}$ Stąd wynika potrzeba zastosowania dwóch płaszczyzn zespolonych, po jednej dla każdego rzutu, które intuicyjnie można skleić „tyłem do siebie” dla ${\displaystyle z=0.}$ Należy zauważyć, że obie płaszczyzny zespolone są odmiennie identyfikowane z płaszczyzną ${\displaystyle z=0.}$ Odwrócona orientacja jest niezbędna aby utrzymać jednoznaczną orientację na sferze, w szczególności sprzężenie zespolone powoduje, że przekształcenia przejścia są holomorficzne.

Przekształcenia przejścia między współrzędnymi ${\displaystyle \zeta }$ i ${\displaystyle \xi ,}$ można uzyskać przez złożenie jednego przekształcenia z odwrotnym do drugiego. Okazuje się, że wynoszą one ${\displaystyle \zeta =1/\xi }$ i ${\displaystyle \xi =1/\zeta ,}$ co jest opisane wyżej. Tym samym sfera jednostkowa jest dyfeomorficzna ze sferą Riemanna.

W tym dyfeomorfizmie, okrąg jednostkowy na mapie ${\displaystyle \zeta }$ oraz okrąg jednostkowy na mapie ${\displaystyle \xi }$ są tożsame z równikiem sfery jednostkowej. Koło jednostkowe ${\displaystyle |\zeta |<1}$ jest tożsame z półsferą południową ${\displaystyle (z<0),}$ a koło jednostkowe ${\displaystyle |\xi |<1}$ jest tożsame z półsferą północną ${\displaystyle (z>0).}$

Zobacz też

• punkt w nieskończoności w geometrii hiperbolicznej

Przypisy

Bibliografia

• Jan Krzyż, Julian Ławrynowicz: Elementy analizy zespolonej. Warszawa: WNT, 1981. ISBN 83-204-0239-5.
• П.С. Александров, П.С. Урысон: Мемуар о компактных топологических пространствах. Москва: Наука, 1971.
• Борис Шабат: Введение в комплексный анализ. T. 1. Москва: Наука, 1985.

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Riemann Sphere, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-03-27].
• Sfera Riemanna na PlanetMath.
• Riemann sphere (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2024-03-27].