Pierwiastek kwadratowy

Ten artykuł dotyczy pierwiastka kwadratowego. Zobacz też: album z 2013.

Pierwiastek kwadratowy – dla danej liczby ${\displaystyle x}$ każda liczba ${\displaystyle r,}$ której kwadrat ${\displaystyle r^{2}}$ jest równy danej liczbie ${\displaystyle x;}$ innymi słowy jest to dowolne rozwiązanie równania (bądź pierwiastek wielomianu) ${\displaystyle r^{2}-x=0}$ zmiennej ${\displaystyle r.}$

Każda dodatnia liczba rzeczywista ${\displaystyle x}$ ma dwa pierwiastki kwadratowe nazywane zbiorczo algebraicznymi: jeden z nich jest dodatni, nazywany często arytmetycznym (pod wyrażeniem „pierwiastek kwadratowy”, czy nawet „pierwiastek” rozumie się często właśnie jego), a drugi – ujemny. Zwykle oznacza się je odpowiednio symbolami ${\displaystyle {\sqrt {x}}}$^[1] bądź ${\displaystyle +{\sqrt {x}}}$ oraz ${\displaystyle -{\sqrt {x}},}$ gdzie ${\displaystyle {\sqrt {\,^{\,}}}}$ jest symbolem pierwiastka; łącznie oznacza się je w skrócie ${\displaystyle \pm {\sqrt {x}}}$ (zob. znak ±). Jedynym pierwiastkiem z liczby ${\displaystyle 0}$ jest ona sama; nie istnieją rzeczywiste pierwiastki kwadratowe z liczb ujemnych (są one urojonymi liczbami zespolonymi). W analizie matematycznej zazwyczaj stosuje się potęgową postać pierwiastka kwadratowego ${\displaystyle x^{1/2}:={\sqrt {x}}.}$

Liczba ${\displaystyle 4}$ jest pierwiastkiem kwadratowym z ${\displaystyle 16,}$ ponieważ ${\displaystyle 4^{2}=4\cdot 4=16;}$ jest ona zarazem arytmetycznym pierwiastkiem kwadratowym tej liczby. Podobnie liczby ${\displaystyle 3}$ oraz ${\displaystyle -3}$ są (algebraicznymi) pierwiastkami kwadratowymi z ${\displaystyle 9,}$ gdyż każda z nich spełnia równanie ${\displaystyle r^{2}=9.}$

Pierwiastki kwadratowe z liczb naturalnych są albo liczbami naturalnymi, albo niewymiernymi. Własność ta była już znana w starożytności, o czym mówi już o tym twierdzenie 9 w księdze X^[2] Elementów Euklidesa. Podejrzewa się, że niewymierność konkretnego przypadku ${\displaystyle {\sqrt {2}}}$ była już znana wcześniej Pitagorejczykom, a za jej odkrywcę tradycyjnie uznawany jest Hippazos^[3].

W ogólności pojęcie pierwiastka (kwadratowego) można rozpatrywać dla przeróżnych obiektów matematycznych, na zbiorze których określone jest działanie dwuargumentowe pełniące rolę mnożenia, np. w algebrze macierzy, czy pierścieniu endomorfizmów (działania odpowiednio mnożenia macierzy i składania funkcji).

W interpretacji geometrycznej dla danego pola powierzchni kwadratu pierwiastek daje długość jego boku; stąd pochodzi nazwa „kwadratowy” (zob. kwadrat (algebra)).

Własności

Dla wszystkich liczb rzeczywistych ${\displaystyle x}$ zachodzi wzór (zob. wartość bezwzględna)

${\displaystyle {\sqrt {x^{2}}}=|x|={\begin{cases}x,&{\text{jeżeli}}x\geqslant 0,\\-x,&{\text{jeżeli}}x<0,\end{cases}}}$

zaś dla wszystkich nieujemnych liczb rzeczywistych ${\displaystyle x}$ oraz ${\displaystyle y}$ prawdziwa jest tożsamość

${\displaystyle {\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}.}$

Ponieważ dla wszystkich liczb zespolonych zachodzi ${\displaystyle |xy|=|x||y|}$ to stosując powyższą tożsamość, zachodzi dla nich również:

${\displaystyle {\sqrt {|xy|}}={\sqrt {|x|}}{\sqrt {|y|}}.}$

Ze wzorów skróconego mnożenia wynikają wzory:

• ${\displaystyle {\sqrt {x}}+{\sqrt {y}}={\sqrt {x+y+2{\sqrt {xy}}}},}$
• ${\displaystyle \left|{\sqrt {x}}-{\sqrt {y}}\right|={\sqrt {x+y-2{\sqrt {xy}}}}.}$

Traktując liczbę podpierwiastkową jako argument funkcji ${\displaystyle f(x)={\sqrt {x}}}$ nazywanej funkcją pierwiastkową, która przekształca zbiór nieujemnych liczb rzeczywistych w siebie, można dowieść, iż jest ona ciągła na całej dziedzinie (dla nieujemnych ${\displaystyle x}$) i różniczkowalna poza zerem (dla dodatnich ${\displaystyle x}$), a jej pierwsza pochodna jest dana wzorem ${\displaystyle f'(x)={\frac {1}{2{\sqrt {x}}}}.}$ Kolejne pochodne dowolnego rzędu dane są dla ${\displaystyle n>0}$ wzorem

${\displaystyle \left({\sqrt {(x)}}\right)^{(n)}=-1^{(n-1)}\cdot {\frac {(2n-3)!!}{2^{n}x^{\frac {2n-1}{2}}}}.}$

Podstawiając pod ten wzór ${\displaystyle n=0}$ otrzymuje się ${\displaystyle {\sqrt {x}},}$ natomiast podstawiając ${\displaystyle n}$ ujemne, otrzymuje się kolejne całki tej funkcji.

Rozwinięcie w szereg Taylora funkcji ${\displaystyle {\sqrt {1+x}}}$ w otoczeniu punktu ${\displaystyle x=0,}$ zbieżny dla ${\displaystyle |x|\leqslant 1,}$ ma postać

${\displaystyle {\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+{\tfrac {1}{2}}x-{\tfrac {1}{8}}x^{2}+{\tfrac {1}{16}}x^{3}-{\tfrac {5}{128}}x^{4}+\dots }$

Obliczanie

 Zobacz też: metody obliczania pierwiastka kwadratowego.

W większości obecnych kalkulatorów kieszonkowych jest dostępny klawisz funkcyjny do wyznaczania arytmetycznego pierwiastka kwadratowego; oprogramowanie komputera przeznaczone do celów obliczeniowych, np. arkusz kalkulacyjny, często dysponuje oddzielną funkcją. Kalkulatory kieszonkowe mają często wydajne implementacje funkcji wykładniczej i logarytmu naturalnego bądź dziesiętnego, które mogą być wykorzystane do obliczania arytmetycznego pierwiastka kwadratowego z dodatniej liczby rzeczywistej za pomocą równania

${\displaystyle {\sqrt {x}}=e^{\frac {\ln x}{2}}\qquad {\text{lub}}\qquad {\sqrt {x}}=10^{\frac {\log x}{2}}.}$

Wzory te mają również zastosowanie dla obliczeń przybliżonych z zastosowaniem tablic logarytmicznych lub suwaka logarytmicznego.

Liczby ujemne i zespolone

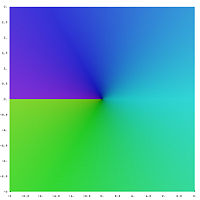
Kwadrat dowolnej liczby dodatniej lub ujemnej jest dodatni, a kwadrat 0 wynosi 0. W związku z tym nie istnieje liczba ujemna, która ma rzeczywisty pierwiastek kwadratowy. Aby znaleźć takie rozwiązania należy rozszerzyć rozważany zbiór liczb na liczby zespolone. Dokonuje się to przez wprowadzenie nowej liczby, oznaczanej przez ${\displaystyle i}$ nazwanej jednostką urojoną, która jest zdefiniowana jako ${\displaystyle i^{2}=-1.}$ Korzystając z tego równania, możemy określić, że ${\displaystyle i}$ to pierwiastek kwadratowy z ${\displaystyle -1,}$ lecz należy zauważyć, że także ${\displaystyle (-i)^{2}=i^{2}=-1,}$ więc ${\displaystyle -i}$ jest także pierwiastkiem kwadratowym z -1. Zgodnie z konwencją, kwadratowy pierwiastek arytmetyczny z ${\displaystyle -1}$ to ${\displaystyle i,}$ lub w ogólności, jeśli ${\displaystyle x}$ jest dowolną liczbą dodatnią, to kwadratowy pierwiastek arytmetyczny z ${\displaystyle -x}$ wynosi

${\displaystyle {\sqrt {-x}}=i{\sqrt {x}}.}$

Prawa strona (a także jej negacja) jest rzeczywiście pierwiastkiem kwadratowym z ${\displaystyle -x,}$ gdyż

${\displaystyle (i{\sqrt {x}})^{2}=i^{2}({\sqrt {x}})^{2}=(-1)x=-x.}$

Dla każdej różnej od 0 liczby zespolonej ${\displaystyle z}$ istnieją dokładnie dwie liczby ${\displaystyle w}$ takie, że ${\displaystyle w^{2}=z{:}}$ kwadratowy pierwiastek arytmetyczny z liczby ${\displaystyle z}$ (zdefiniowany poniżej) i jego negacja.

Pierwiastek kwadratowy z liczby urojonej

Pierwiastek kwadratowy z ${\displaystyle i}$ jest dany wzorem

${\displaystyle {\sqrt {i}}={\tfrac {1}{2}}{\sqrt {2}}+i{\tfrac {1}{2}}{\sqrt {2}}={\tfrac {\sqrt {2}}{2}}(1+i).}$

Wynik ten można otrzymać algebraicznie przez znalezienie ${\displaystyle a}$ i ${\displaystyle b}$ w sposób

${\displaystyle i=(a+bi)^{2}}$

lub odpowiednio

${\displaystyle i=a^{2}+2abi-b^{2}.}$

Co daje układ dwóch równań

${\displaystyle {\begin{cases}2ab=1\\a^{2}-b^{2}=0\end{cases}}}$

z rozwiązaniami

${\displaystyle a=b=\pm {\tfrac {1}{\sqrt {2}}}.}$

Dla arytmetycznego pierwiastka kwadratowego wybieramy

${\displaystyle a=b={\tfrac {1}{\sqrt {2}}}.}$

Ten wynik można również uzyskać, korzystając ze wzoru de Moivre’a, podstawiając

${\displaystyle i=\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}},}$

który daje

${\displaystyle {\sqrt {i}}=\left(\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}}\right)^{\frac {1}{2}}=\cos {\tfrac {\pi }{4}}+i\sin {\tfrac {\pi }{4}}={\tfrac {1}{\sqrt {2}}}+i{\tfrac {1}{\sqrt {2}}}={\tfrac {1+i}{\sqrt {2}}}.}$

Kwadratowy pierwiastek arytmetyczny z liczby zespolonej

Aby znaleźć definicję pierwiastka kwadratowego, która jednoznacznie określi jedną wartość, zwaną kwadratowym pierwiastkiem arytmetycznym, należy zauważyć, że liczbę zespoloną ${\displaystyle x+iy}$ można przedstawić jako punkt na płaszczyźnie ${\displaystyle (x,y),}$ wyrażoną w układzie współrzędnych kartezjańskich. Ten sam punkt może być odczytany za pomocą współrzędnych biegunowych jako para ${\displaystyle (r,\varphi ),}$ gdzie ${\displaystyle r\geqslant 0}$ jest odległością od środka układu współrzędnych, a ${\displaystyle \varphi }$ to kąt jaki tworzy półprosta o początku w środku układu współrzędnych i przechodząca przez zadany punkt z półosią dodatnich ${\displaystyle x,}$ wartość ta jest zwykle zapisywana ${\displaystyle r\,e^{i\varphi }.}$

Jeśli

${\displaystyle z=r\,e^{\varphi i}}$

oraz

${\displaystyle -\pi <\varphi \leqslant \pi ,}$

to kwadratowy pierwiastek arytmetyczny z liczby ${\displaystyle z}$ definiuje się wzorem

${\displaystyle {\sqrt {z}}={\sqrt {r}}\,e^{i\varphi /2}.}$

Oś rzeczywista dla wartości niedodatnich tworzy wtedy zbiór punktów rozgałęzienia. Funkcja kwadratowego pierwiastka arytmetycznego jest wszędzie holomorficzna z wyjątkiem rzeczywistych liczb niedodatnich (ściślej ujmując, dla ujemnych liczb rzeczywistych nie jest nawet ciągła). Powyższy szereg Taylora dla ${\displaystyle {\sqrt {1+x}}}$ pozostaje słuszny dla liczb zespolonych ${\displaystyle x}$ gdzie ${\displaystyle |x|<1.}$

Powyższe równanie można także wyrazić za pomocą funkcji trygonometrycznych:

${\displaystyle {\sqrt {r\left(\cos \varphi +i\sin \varphi \right)}}={\sqrt {r\left(\cos {\tfrac {\varphi }{2}}+i\sin {\tfrac {\varphi }{2}}\right)}}.}$

Wzór algebraiczny

Kiedy liczba jest wyrażona we współrzędnych kartezjańskich, to za pomocą następującego wzoru można wyznaczyć kwadratowy pierwiastek arytmetyczny^[4][5]:

${\displaystyle {\sqrt {x+iy}}=\pm {\sqrt {\frac {|z|+x}{2}}}\pm \operatorname {sgn}(y)i{\sqrt {\frac {|z|-x}{2}}},}$

gdzie sgn to funkcja zwracająca znak, a ${\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}$ to moduł liczby zespolonej.

Wyprowadzenie

Oznaczmy ${\displaystyle {\sqrt {z}}=\pm (a+ib)}$ oraz ${\displaystyle a={\sqrt {\frac {|z|+x}{2}}}}$ oraz ${\displaystyle b=\operatorname {sgn}(y){\sqrt {\frac {|z|-x}{2}}}}$ Sprawdzenie: ${\displaystyle x+iy=z=({\sqrt {z}})^{2}=(\pm (a+ib))^{2}=a^{2}+2abi-b^{2}}$ Rozpatrzmy część rzeczywistą ostatniej równości ${\displaystyle a^{2}-b^{2}=\left({\sqrt {\frac {|z|+x}{2}}}\right)^{2}-\left(\operatorname {sgn}(y){\sqrt {\frac {|z|-x}{2}}}\right)^{2}={\frac {|z|+x}{2}}-{\frac {|z|-x}{2}}={\frac {2x}{2}}=x}$ oraz część urojoną (korzystamy z własności kwadratu modułu: ${\displaystyle |z|^{2}=x^{2}+y^{2}}$): ${\displaystyle 2ab=2\left({\sqrt {\frac {|z|+x}{2}}}\right)\left(\operatorname {sgn}(y){\sqrt {\frac {|z|-x}{2}}}\right)=2\operatorname {sgn}(y){\sqrt {\frac {(|z|+x)(|z|-x)}{4}}}=2\operatorname {sgn}(y){\frac {1}{2}}{\sqrt {|z|^{2}-x^{2}}}}$ ${\displaystyle =\operatorname {sgn}(y){\sqrt {x^{2}+y^{2}-x^{2}}}=\operatorname {sgn}(y){\sqrt {y^{2}}}=\operatorname {sgn}(y)|y|=y}$ Gdy powyższe ciągi równości rozpatrzymy od końca, niniejsze sprawdzenie staje się wyprowadzeniem.

Wzór na iloczyn pierwiastków

Z powodu nieciągłości funkcji pierwiastka kwadratowego na płaszczyźnie zespolonej, ogólna reguła ${\displaystyle {\sqrt {zw}}={\sqrt {z}}{\sqrt {w}}}$ nie jest spełniona (podobny problem występuje przy obliczaniu logarytmu liczby zespolonej). Błędne założenie, co to słuszności tej reguły może prowadzić do fałszywych „dowodów”, jak np. poniższy pokazujący, że

${\displaystyle -1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {-1\cdot -1}}={\sqrt {1}}=1.}$

Przekształcenie w trzeciej równości nie może być zastosowane. Mogłoby być one zastosowane pod warunkiem zmiany znaczenia √ na takie, że jego rozwiązaniem nie jest już pierwiastek kwadratowy arytmetyczny, ale funkcja zawierająca ${\displaystyle ({\sqrt {-1}})({\sqrt {-1}}).}$ Wobec czego lewa strona staje się również

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}=i\cdot i=-1,}$

jeśli zbiór zawiera ${\displaystyle +i}$ lub

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}=(-i)\cdot (-i)=-1,}$

jeśli zbiór zawiera ${\displaystyle -i,}$ podczas gdy prawa strona staje się

${\displaystyle {\sqrt {-1\cdot -1}}={\sqrt {1}}=-1,}$

gdzie ostatnia równość, ${\displaystyle {\sqrt {1}}=-1}$ jest konsekwencją wyboru ze zbioru w nowej definicji pierwiastka.

Zobacz też

• pierwiastek kwadratowy z 2
• pierwiastek kwadratowy z 3
• pierwiastek kwadratowy z 5
• pierwiastek sześcienny i pierwiastkowanie
• pierwiastek z jedynki
• reszta kwadratowa modulo
• niereszta kwadratowa modulo

Przypisy